7. Max-Min Problems

Exercises

a. Local Minima, Local Maxima and Saddle Points

1

2

3

4

Find all critical points of each function. Then use the Second Derivative Test to classify each as a local minimum, local maximum or saddle or say the test fails.

1. \(f(x,y)=(x+3)^2+(y-1)^2\)

   Set the \(x\)-derivative and the \(y\)-derivative equal to zero and solve for \(x\) and \(y\). \[\begin{aligned} f_x(x,y)&=\dfrac{\partial f}{\partial x}=0 \\ f_y(x,y)&=\dfrac{\partial f}{\partial y}=0 \end{aligned}\]

   The critical point, \((-3,1)\), is a local minimum.

   We compute the partial derivatives, set them equal to \(0\) and solve for \(x\) and \(y\): \[\begin{aligned} f_x=2(x+3)=0 \qquad &\Longrightarrow& \qquad x=-3 \\ f_y=2(y-1)=0 \qquad &\Longrightarrow& \quad y=1 \end{aligned}\] So the critical point is \((x,y)=(-3,1)\). \[ f_{xx}=2 \qquad f_{yy}=2 \qquad f_{xy}=0 \qquad D=f_{xx}f_{yy}-{f_{xy}}^2=4 \] Since \(D=4 \gt 0\) and \(f_{xx}=2 \gt 0\) the critical point is a local minimum.

   This should have been obvious, since the function is an elliptic paraboloid opening upward with vertex at \((-3,1)\).

2. \(z=4xy+2y\)

   The critical point, \((x,y)=\left(-\,\dfrac{1}{2},0\right)\), is a saddle.

   \[\begin{aligned} \dfrac{\partial z}{\partial x}=4y=0 \qquad &\Longrightarrow& \quad y=0 \\ \dfrac{\partial z}{\partial y}=4x+2=0 \qquad &\Longrightarrow& \quad x=-\,\dfrac{1}{2} \end{aligned}\] The critical point is \((x,y)=\left(-\,\dfrac{1}{2},0\right)\). \[ f_{xx}=0 \qquad f_{yy}=0 \qquad f_{xy}=4 \qquad D=f_{xx}f_{yy}-{f_{xy}}^2=-16 \] Since \(D=-16 \lt 0\), the critical point is a saddle.

3. \(g(x,y)=3x^2y+2xy^2\)

   The only critical point is \((0,0)\) for which the test fails.

   \[\begin{aligned} g_x=6xy+2y^2=2y(3x+y)=0 \qquad &\Longrightarrow& \qquad y=0 \qquad \text{or} \qquad y=-3x \\ g_y=3x^2+4xy=x(3x+4y)=0 \qquad &\Longrightarrow& \qquad x=0 \qquad \text{or} \qquad y=-\,\dfrac{3x}{4} \end{aligned}\] There are four cases. Three lead to the critical point \((x,y)=(0,0)\). The fourth \(y=-3x=-\,\dfrac{3x}{4}\) is a contradiction unless \(x=y=0\) again. We apply the Second Derivative test: \[ g_{xx}=6y \qquad g_{yy}=4x \qquad g_{xy}=6x+4y \] So \[ g_{xx}(0,0)=0 \qquad g_{yy}(0,0)=0 \qquad g_{xy}(0,0)=0 \qquad D=0 \] Since \(D=0\), the test fails.

4. \(p(u,v)=3u^2-uv^2+v^3\)

   The critical point \((u,v)=\left(\dfrac{27}{2},9\right)\) is a local minimum.
   The test fails for the critical point \((u,v)=(0,0)\).

   \[\begin{aligned} p_u&=6u-v^2=0 \qquad \text{(1)} \\ p_v&=-2uv+3v^2=v(-2u+3v)=0 \qquad \text{(2)} \end{aligned}\] Equation (2) leads to \(2\) cases:

   • Case 1: \(v=0\): Then equation (1) says \(u=0\) and gives the critical point \((u,v)=(0,0)\).
   • Case 2: \(v=\dfrac{2}{3}u\): Then equation (1) says \(6u-\,\dfrac{4}{9}u^2=0\) or \(u\left(6-\,\dfrac{4}{9}u\right)=0\) which leads to \(2\) cases:
   • Case 2a: \(u=0\) which repeats the critical point \((u,v)=(0,0)\).
   • Case 2b: \(u=\dfrac{27}{2}\) and hence \(v=9\) and the critical point \((u,v)=\left(\dfrac{27}{2},9\right)\)

   The second derivatives are: \[ p_{uu}=6 \qquad p_{vv}=2u+6v \qquad p_{uv}=-2v \] We make a table to keep track of the values.

   \(u\)	\(v\)	\(p_{uu}\)	\(p_{vv}\)	\(p_{uv}\)	\(D\)	Classification
   \(0\)	\(0\)	\(6\)	\(0\)	\(0\)	\(0\)	test fails
   \(\dfrac{27}{2}\)	\(9\)	\(6\)	\(81\)	\(-18\)	\(162\)	minimum

5. \(f(x,y)=x^2+2y^2+xy+4x-5y\)

   The critical point, \((x,y)=(-3,2)\), is a local minimum.

   To find the critical points, we set the partial derivatives equal to \(0\) and solve: \[\begin{aligned} f_x&=2x+y+4&=0 \qquad \text{(1)} \\ f_y&=x+4y-5&=0 \qquad \text{(2)} \end{aligned}\] Equation (1) minus \(2\) times equation (2) gives \(-7y+14=0\). So \(y=2\). Then equation (2) says \(x=5-4y=-3\). This gives the critical point \((-3,2)\). The second derivatives are: \[ f_{xx}=2 \qquad f_{yy}=4 \qquad f_{xy}=1 \qquad D=2\cdot4-1^2=7 \] Since \(D \gt 0\) and \(f_{xx} \gt 0\) the critical point is a local minimum.

6. \(f(x,y)=2x^2y+2xy^2-3y^2\)

   The critical point \((u,v)=(2,-4)\) is a saddle point.
   The test fails for the critical point \((u,v)=(0,0)\).

   To find the critical points, we set the partial derivatives equal to \(0\) and solve: \[\begin{aligned} f_x&=4xy+2y^2&=0 \qquad \text{(1)} \\ f_y&=2x^2+4xy-6y&=0 \qquad \text{(2)} \end{aligned}\] Equation (1) factors as \(y(4x+2y)=0\). This gives us two cases:

   • Case 1: \(y=0\): Then equation (2) reduces to \(2x^2=0\) or \(x=0\). This gives the critical point \((0,0)\).
   • Case 2: \(y=-2x\): Then equation (2) reduces to \(2x^2-8x^2+12x=0\) which factors as \(6x(-x+2)=0\). This gives two cases: \(x=0\) and \(x=2\). These give the the critical points \((0,0)\) and \((2,-4)\).

   The second derivatives are: \[ f_{xx}=4y \qquad f_{yy}=4x-6 \qquad f_{xy}=4x+4y \] We make a table to keep track of the values.

   \(x\)	\(y\)	\(f_{xx}\)	\(f_{yy}\)	\(f_{xy}\)	\(D\)	Classification
   \(0\)	\(0\)	\(0\)	\(-6\)	\(0\)	\(0\)	test fails
   \(2\)	\(-4\)	\(-16\)	\(2\)	\(-8\)	\(-96\)	saddle point

7. \(f(x,y,z)=2x^3+3x^2y+3x^2z+3x^2+y^2-z^2+2yz-3y+9z\)

   The \(3\) critical points, \[ \left(0,-\,\dfrac{3}{2},3\right) \qquad (-1,-3,3) \qquad \left(\dfrac{5}{3},-\,\dfrac{17}{3},3\right) \] are all saddle points.

   To find the critical points, we set the partial derivatives equal to \(0\) and solve: \[\begin{aligned} f_x&=6x^2+6xy+6xz+6x&=0 \qquad \text{(1)} \\ f_y&=3x^2+2y+2z-3&=0 \qquad \text{(2)} \\ f_z&=3x^2+2y-2z+9&=0 \qquad \text{(3)} \end{aligned}\] First notice that equation (2) minus equation (3) gives \(4z-12=0\) or \(z=3\). Then equation (2) or (3) reduces to: \[ 3x^2+2y+3=0 \qquad \text{(4)} \] Next notice that equation (1) factors as \(6x(x+y+z+1)=0\). This gives \(2\) cases:

   • Case 1: \(x=0\): Then equation (4) reduces to \(2y+3=0\) or \(y=-\,\dfrac{3}{2}\). This gives the critical point \(\left(0,-\,\dfrac{3}{2},3\right)\).
   • Case 2: \(x+y+z+1=0\): Using \(z=3\), this says \(x=-y-4\). So equation (4) becomes \(3(-y-4)^2+2y+3=0\) which expands to \[ 3y^2+26y+51=0 \] which has the solutions \(y=-3\) and \(y=-\,\dfrac{17}{3}\). This gives two critical points \((-1,-3,3)\) and \(\left(\dfrac{5}{3},-\,\dfrac{17}{3},3\right)\).

   To apply the Second Derivative Test, we need the Hessian: \[ \text{Hess}f=\begin{pmatrix} f_{xx} & f_{xy} & f_{xz} \\ f_{yx} & f_{yy} & f_{yz} \\ f_{zx} & f_{zy} & f_{zz} \\ \end{pmatrix} =\begin{pmatrix} 12x+6y+6z+6 & 6x & 6x \\ 6x & 2 & 2 \\ 6x & 2 & -2 \\ \end{pmatrix} \] We evaluate at each critical point:

   • At \(\left(0,-\,\dfrac{3}{2},3\right)\), \[ \text{Hess}f=\begin{pmatrix} 15 & 0 & 0 \\ 0 & 2 & 2 \\ 0 & 2 & -2 \\ \end{pmatrix} \] The Leading Principal Minor Determinants are \[ D_1=15\qquad D_2=30 \qquad D_3=-120 \] They are not all positive and they do not alternate signs and \(D_3\ne0\). So this is a saddle point.
   • At \((-1,-3,3)\), \[ \text{Hess}f=\begin{pmatrix} -6 & -6 & -6 \\ -6 & 2 & 2 \\ -6 & 2 & -2 \\ \end{pmatrix} \] The Leading Principal Minor Determinants are \[ D_1=-6\qquad D_2=-48 \qquad D_3=192 \] So this is also a saddle point.
   • At \(\left(\dfrac{5}{3},-\,\dfrac{17}{3},3\right)\), \[ \text{Hess}f=\begin{pmatrix} 10 & 10 & 10 \\ 10 & 2 & 2 \\ 10 & 2 & -2 \\ \end{pmatrix} \] The Leading Principal Minor Determinants are \[ D_1=10\qquad D_2=-80 \qquad D_3=320 \] Again this is a saddle point.

8. \(g(x,y)=x^3-y^3-6xy\)

   The critical point, \((x,y)=(0,0)\), is a saddle point.
   The critical point, \((x,y)=(-2,2)\), is a local maximum.

   To find the critical points, we set the partial derivatives equal to \(0\) and solve: \[\begin{aligned} g_x&=3x^2-6y&=0 \qquad \text{(1)} \\ g_y&=-3y^2-6x&=0 \qquad \text{(2)} \end{aligned}\] Solving equation (1) for \(y\) gives the equation \(y=\dfrac{x^2}{2}\). Plugging this into equation (2) gives: \[\begin{aligned} -3\left(\dfrac{x^2}{2}\right)^2-6x&=0 \\ x^4+8x&=0 \\ x(x^3+8)&=0 \end{aligned}\] So the solutions are \((x,y)=(0,0)\) and \((x,y)=(-2,2)\).

   The second derivatives are: \[ g_{xx}=6x \qquad g_{yy}=-6y \qquad g_{xy}=-6 \] We make a table of values:

   \(x\)	\(y\)	\(g_{xx}\)	\(g_{yy}\)	\(g_{xy}\)	\(D\)	Classification
   \(0\)	\(0\)	\(0\)	\(0\)	\(-6\)	\(-36\)	Saddle Point
   \(-2\)	\(2\)	\(-12\)	\(-12\)	\(-6\)	\(108\)	Local Maximum

   wll 

9. \(f(x,y)=3x^2+6xy-2y^3+6y^2\)

   The critical point, \((x,y)=(0,0)\), is a local minimum.
   The critical point, \((x,y)=(-1,1)\), is a saddle point.

   To find the critical points, we set the partial derivatives equal to \(0\) and solve: \[\begin{aligned} f_x&=6x+6y&=0 \qquad \text{(1)} \\ f_y&=6x-6y^2+12y&=0 \qquad \text{(2)} \end{aligned}\] Subtracting equation (2) from equation (1) results in the equation \(6y^2-6y=0\) which factors as \(y(y-1)=0\). So the solutions are \(y=0\) and \(y=1\).

   • Case 1: \(y=0\): Plugging this into equation (1) yields \(x=0\) and the critical point \((0,0)\).
   • Case 2: \(y=1\): Plugging this into equation (1) yields \(x=-1\) and the critical point \((-1,1)\).

   The second derivatives are: \[ f_{xx}=6 \qquad f_{yy}=-12y+12 \qquad f_{xy}=6 \] We make a table:

   \(x\)	\(y\)	\(f_{xx}\)	\(f_{yy}\)	\(f_{xy}\)	\(D\)	Classification
   \(0\)	\(0\)	\(6\)	\(12\)	\(6\)	\(36\)	Local Minimum
   \(-1\)	\(1\)	\(6\)	\(0\)	\(6\)	\(-36\)	Saddle Point

   wll 

10. \(g(x,y)=x^3+y^3-12xy\)

    The critical point, \((x,y)=(0,0)\), is a Saddle Point.
    The critical point, \((x,y)=(4,4)\), is a Local Minimum.

    To find the critical points, we set the partial derivatives equal to \(0\) and solve: \[\begin{aligned} g_x&=3x^2-12y&=0 \qquad \text{(1)} \\ g_y&=3y^2-12x&=0 \qquad \text{(2)} \end{aligned}\] Solving for \(y\) in equation (1) gives \(y=\dfrac{x^2}{4}\). Plugging this into equation (2) gives: \[\begin{aligned} 3\left( \dfrac{x^2}{4} \right)^2 -12x = 0 \\ x^4-64x=0 \\ x(x^3-64) = 0 \end{aligned}\] So the solutions are \((x,y)=(0,0)\) and \((x,y)=(4,4)\).
    The second derivatives are: \[ g_{xx}=6x \qquad g_{yy}=6y \qquad g_{xy}=-12 \] We make a table of values:

    \(x\)	\(y\)	\(g_{xx}\)	\(g_{yy}\)	\(g_{xy}\)	\(D\)	Classification
    \(0\)	\(0\)	\(0\)	\(0\)	\(-12\)	\(-144\)	Saddle Point
    \(4\)	\(4\)	\(24\)	\(24\)	\(-12\)	\(432\)	Local Minimum

    wll 

11. \(f(x,y)=x^3+y^3-3x^2+3y^2\)

    The critical point, \((x,y)=(0,0)\), is a saddle point.
    The critical point, \((x,y)=(0,-2)\), is a local maximum.
    The critical point, \((x,y)=(2,0)\), is a local minimum.
    The critical point, \((x,y)=(2,-2)\), is a saddle point.

    To find the critical points, we set the partial derivatives equal to \(0\) and solve: \[\begin{aligned} f_x&=3x^2-6x&=0 \qquad \text{(1)} \\ f_y&=3y^2+6y&=0 \qquad \text{(2)} \end{aligned}\] Since each first partial derivatve is a function of only one variable, We can solve them separately.
    Equation (1) factors as \(3x(x-2)=0\). The solutions are \(x=0,2\).
    Equation (2) factors as \(3y(y+2)=0\). The solutions are \(y=0,-2\).
    So there are \(4\) critical points: \[ (0,0) \qquad (0,-2) \qquad (2,0) \qquad (2,-2) \]

    The second derivatives are: \[\begin{aligned} f_{xx}=6x-6 \qquad f_{yy}=6y+6 \qquad f_{xy}=0 \end{aligned}\] We make a table:

    \(x\)	\(y\)	\(f_{xx}\)	\(f_{yy}\)	\(f_{xy}\)	\(D\)	Classification
    \(0\)	\(0\)	\(-6\)	\(6\)	\(0\)	\(-36\)	Saddle Point
    \(0\)	\(-2\)	\(-6\)	\(-6\)	\(0\)	\(36\)	Local Maximum
    \(2\)	\(0\)	\(6\)	\(6\)	\(0\)	\(36\)	Local Minimum
    \(2\)	\(-2\)	\(6\)	\(-6\)	\(0\)	\(-36\)	Saddle Point

    wll 

12. \(g(x,y)=x^4+y^4-4xy\)

    The critical point, \((x,y)=(0,0)\), is a saddle point.
    The critical point, \((x,y)=(-1,-1)\), is a local minimum.
    The critical point, \((x,y)=(1,1)\), is a local minimum.

    To find the critical points, we set the partial derivatives equal to \(0\) and solve: \[\begin{aligned} g_x&=4x^3 - 4y&=0 \qquad \text{(1)} \\ g_y&=4y^3 - 4x&=0 \qquad \text{(2)} \end{aligned}\] Solving equation (1) for \(y\) yields \(y=x^3\). Plugging this into equation (2) gives: \[\begin{aligned} 4\left(x^3\right)^3 - 4x = 0 \\ x(x^8 - 1) = 0 \end{aligned}\] Solutions are \(x = 0\) and \(x = \pm 1\). So the \(3\) critical points are: \[ (0,0) \qquad (-1,-1) \qquad (1,1) \]

    The second derivatives are: \[ g_{xx}=12x^2 \qquad g_{yy}=12y^2 \qquad g_{xy}=-4 \] We make a table of values:

    \(x\)	\(y\)	\(g_{xx}\)	\(g_{yy}\)	\(g_{xy}\)	\(D\)	Classification
    \(0\)	\(0\)	\(0\)	\(0\)	\(-4\)	\(-16\)	Saddle Point
    \(-1\)	\(-1\)	\(12\)	\(12\)	\(-4\)	\(128\)	Local Minimum
    \(1\)	\(1\)	\(12\)	\(12\)	\(-4\)	\(128\)	Local Minimum

    wll 

13. \(f(x,y)=x^4+y^4+4xy\)

    The critical point, \((x,y)=(0,0)\), is a saddle point.
    The critical point, \((x,y)=(-1,1)\), is a local minimum.
    The critical point, \((x,y)=(1,-1)\), is a local minimum.

    To find the critical points, we set the partial derivatives equal to \(0\) and solve: \[\begin{aligned} f_x&=4x^3 + 4y&=0 \qquad \text{(1)} \\ f_y&=4y^3 + 4x&=0 \qquad \text{(2)} \end{aligned}\] Solving equation (1) for \(y\) yields \(y=-x^3\). Plugging this into equation (2) gives: \[\begin{aligned} 4\left(-x^3\right)^3 + 4x = 0 \\ -4x^9+4x = 0 \\ x(-x^8 + 1) = 0 \end{aligned}\] Solutions are \(x = 0\) and \(x = \pm 1\). So the \(3\) critical points are: \[ (0,0) \qquad (-1,1) \qquad (1,-1) \]

    The second derivatives are: \[ f_{xx}=12x^2 \qquad f_{yy}=12y^2 \qquad f_{xy}=4 \] We make a table of values:

    \(x\)	\(y\)	\(f_{xx}\)	\(f_{yy}\)	\(f_{xy}\)	\(D\)	Classification
    \(0\)	\(0\)	\(0\)	\(0\)	\(4\)	\(-16\)	Saddle Point
    \(-1\)	\(1\)	\(12\)	\(12\)	\(4\)	\(128\)	Local Minimum
    \(1\)	\(-1\)	\(12\)	\(12\)	\(4\)	\(128\)	Local Minimum

    wll 

b. Constrained Max-Min Problems

1

2

3

14. Find the dimensions and volume of the largest box with base on the \(xy\) plane and upper vertices on the paraboloid \(z=16-2x^2-y^2\).
    Solve by eliminating \(z\).

    

    The length, width and height are not just \(x\), \(y\) and \(z\).

    The length, width, height and volume are: \[ L=2\sqrt{2} \qquad W=4 \qquad H=8 \qquad V=LWH=64\sqrt{2} \]

    The volume of the box is given by \[ V=(2x)(2y)(z)=4xyz \] where \(x\), \(y\) and \(z\) are the coordinates of the vertex of the box in the first quadrant. We can eliminate a variable by substituting the constraint equation \(z=16-2x^2-y^2\): \[ V=4xy(16-2x^2-y^2)=64xy-8x^3y-4xy^3 \] Next we set the \(x\) and \(y\) partial derivatives equal to zero and solve for \(x\) and \(y\): \[\begin{aligned} f_x&=64y-24x^2y-4y^3=4y(16-6x^2-y^2)=0 \\ f_y&=64x-8x^3-12xy^2=4x(16-2x^2-3y^2)=0 \end{aligned}\] If \(x=0\) or \(y=0\), then the volume would be \(0\) which would not be the maximum. So taking \(x\neq 0\) and \(y\neq 0\), we have \[\begin{aligned} 6x^2+y^2&=16 \qquad \text{(1)} \\ 2x^2+3y^2&=16 \qquad \text{(2)} \end{aligned}\] We compute \(3\) times equation (1) minus equation (2): \[ 16x^2=32 \quad \Longrightarrow \qquad x=\sqrt{2} \] Similarly, \(3\) times equation (2) minus equation (1) gives: \[ 8y^2=32 \quad \Longrightarrow \qquad y=2 \] (We ignored the \(\pm\) because we want \((x,y)\) in the first quadrant.) We plug into the parabola: \[ z=16-2x^2-y^2=16-4-4=8 \] So the length, width, height and volume are: \[\begin{aligned} L=2x=2\sqrt{2} \qquad &W=2y=4 \qquad H=z=8 \\ V=&LWH=64\sqrt{2} \end{aligned}\]

    py,tj 

15. Find the point on the plane \(2x-2y-z=18\) that is closest to the origin. Then find the distance from the point to the origin.
    Solve by eliminating \(z\).
    Rotate the second plot with your mouse.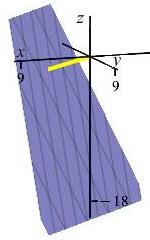

    

    It is easier to minimize the square of the distance than the actual distance. The answer will be the same.

    The closest point is \((x,y,z)=(4,-4,-2)\).
    Its distance from the origin is \(D=6\).

    We need to minimize the distance from the origin to the point \((x,y,z)\) on the plane \[ D=\sqrt{x^2+y^2+z^2} \] It is easier to minimize the square of the distance, which will give the same solution. So we will minimize the function \[ f=D^2=x^2+y^2+z^2 \] Since the point must lie on the plane, we substitute the equation of the plane \(z=2x-2y-18\) into \(f\): \[ f=x^2+y^2+(2x-2y-18)^2 \] We take the \(x\) and \(y\) derivatives and set them equal to zero: \[\begin{aligned} f_x&=2x+4(2x-2y-18)=10x-8y-72=0 \\ f_y&=2y-4(2x-2y-18)=-8x+10y+72=0 \end{aligned}\] Equivalently: \[\begin{aligned} 5x-4y&=36 \qquad \text{(1)} \\ -4x+5y&=-36 \qquad \text{(2)} \end{aligned}\] Multiply the first equation by \(4\) and the second equation by \(5\) and add: \[\begin{aligned} 20x-16y&=144 \\ -20x+25y&=-180 \\ 9y&=-36 \qquad \Longrightarrow \qquad y=-4 \end{aligned}\] Substituting back we have: \[ 5x-4(-4)=36 \qquad \Longrightarrow \qquad x=4 \] \[ z=2x-2y-18=2(4)-2(-4)-18=-2 \] So the closest point is \((x,y,z)=(4,-4,-2)\). Its distance from the origin is \[ D=\sqrt{16+16+4}=6 \]

    py,tj 

16. Find the dimensions and volume of the largest box with base on the \(xy\) plane and upper vertices on the paraboloid \(z=16-2x^2-y^2\).
    Solve by using a Lagrange multiplier.

    

    What are the length, width and height in terms of the point \((x,y,z)\) on the paraboloid in the first octant.

    The length, width, height and volume are:
    \( L=2\sqrt{2} \qquad W=4 \qquad H=8 \)
    \( V=64\sqrt{2} \)

    We need to maximize the volume. If we take the point \((x,y,z)\) in the first octant, the height is \(H=z\), but the length and width need to be doubled: \(L=2x\) and \(W=2y\). So the volume is \(V=LWH=4xyz\). This is subject to the constraint that the point \((x,y,z)\) lies on the paraboloid, \(g=z+2x^2+y^2=16\). The gradients are: \[\begin{aligned} \vec\nabla V&=\langle 4yz,4xz,4xy \rangle \\ \vec\nabla g&=\langle 4x,2y,1 \rangle \end{aligned}\] So the Lagrange equations, \(\vec\nabla V=\lambda\vec\nabla g\), are: \[\begin{aligned} 4yz&=\lambda 4x \qquad \text{(1)} \\ 4xz&=\lambda 2y \qquad \text{(2)} \\ 4xy&=\lambda \qquad \text{(3)} \end{aligned}\] We multiply (1) by \(x\), (2) by \(y\), (3) by \(z\) and equate the left hand sides: \[ 4xyz=\lambda 4x^2=\lambda 2y^2=\lambda z \] This says \(x^2=\dfrac{z}{4}\) and \(y^2=\dfrac{z}{2}\). We plug these into the constraint: \[ 16=z+2x^2+y^2=z+\dfrac{z}{2}+\dfrac{z}{2}=2z \] So \[ z=8 \qquad x=\sqrt{2} \qquad y=2 \] So the length, width, height and volume are: \[\begin{aligned} L=2x=2\sqrt{2} \qquad &W=2y=4 \qquad H=z=8 \\ V=&LWH=64\sqrt{2} \end{aligned}\]

    Notice that this is the same problem as previously solved. There we eliminated a variable. Here we used Lagrange mumtipliers.

17. Find the radius of the sphere with its center at the origin which is tangent to the plane \(2x-2y-z=18\).
    Solve by using a Lagrange multiplier.
    Rotate the second plot with your mouse.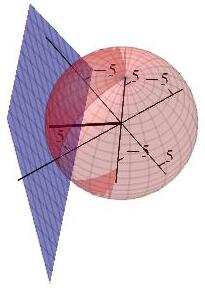

    

    The radius of the sphere is the shortest distance to the plane. It is easier to minimize the square of the distance.

    The radius is \(r=6\).

    The radius of the sphere is the shortest distance to the plane. We minimize the square of the distance: \[ f=D^2=x^2+y^2+z^2 \] subject to the constraint that the point is on the plane: \[ g=2x-2y-z=18 \] The gradients are \[ \vec\nabla f=\langle 2x,2y,2z \rangle \qquad \vec\nabla g=\langle 2,-2,-1 \rangle \] The Lagrange equations, \(\vec\nabla f=\lambda\vec\nabla g\), are \[ 2x=2\lambda \qquad 2y=-2\lambda \qquad 2z=-\lambda \] Consequently, \(\lambda=x=-y=-2z\). Plug these into the constraint: \[ 18=2x-2y-z=-4z-4z-z=-9z \qquad \Longrightarrow \qquad z=-2 \] So \(x=4\), \(y=-4\) and the point of tangency is \((x,y,z)=(4,-4,-2)\). So the radius is: \[ r=\sqrt{4^2+4^2+2^2}=6 \]

    tj 

    Notice that this is effectively the same problem as previously solved because in both cases we are minimizing the distance from the origin to the plane. There we eliminated a variable. Here we used Lagrange mumtipliers.

18. Find the point(s) on the hyperbolic cylinder \(z^2-y^2=1\) closest to the origin.

    Only find the real solutions when solving the Lagrange equations.

    \((0, 0, -1)\) and \((0, 0, 1)\)

    We minimize the square of the distance function from the origin using \(f=D^2 = x^2+y^2+z^2\) on the hyperbolic cylinder \(g= z^2-y^2=1\). The gradients of the functions are \[\begin{aligned} \vec\nabla f &=\langle 2x, 2y, 2z\rangle \\ \vec\nabla g&=\langle0,-2y,2z\rangle \end{aligned}\] The Lagrange equations, \(\vec\nabla f=\lambda\vec\nabla g\), are \[\begin{aligned} 2x&=0 \qquad \text{(1)} \\ 2y&=-2\lambda y \qquad \text{(2)} \\ 2z&=2\lambda z \qquad \text{(3)} \end{aligned}\] Equation (1) yields \(x = 0\). Factoring equation (2) gives: \[ y \left(2+2\lambda \right)=0 \] The two solution are \(y=0\) and \(\lambda=-1\).
    Case 1: Plugging \(y=0\) into the constraint equation \(z^2-y^2=1\), gives: \[ z = \pm 1 \] and equation (3) gives \(\lambda=1\)..
    Case 2: Plugging \(\lambda=-1\) into equation (3), gives \(z=-z\) which says \(z=0\). Then the constraint \(z^2-y^2=1\) gives \(-y^2=1\) which only has imaginary solutions.
    So the two critical points are: \[ (0, 0, -1) \quad\text{and} \quad (0, 0, 1) \] which are at a distance \(D=\sqrt{0^2+0^2+1^2}=1\) from the origin. Any other point would have \(z^2=1+y^2 \ge 1\) and so a bigger distance.

    wll 

19. Find the largest and smallest values of the function \(f(x,y)=xy\) on the ellipse \(\dfrac{x^2}{18}+\dfrac{y^2}{8}=1\).

    

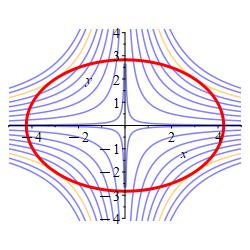
    Find the gradients of both functions.

    The smallest value of \(f(x,y) = xy\) along the ellipse is \(-6\).
    The largest value of \(f(x,y) = xy\) along the ellipse is \(6\).

    We maximize and minimize the function \(f=xy\) with the constraint of the ellipse \(g= \dfrac{x^2}{18}+\dfrac{y^2}{8}=1\).
    
    The gradients of the functions are \[ \vec\nabla f=\langle y,x \rangle \qquad \vec\nabla g=\left\langle \dfrac{x}{9},\dfrac{y}{4} \right\rangle \] The Lagrange equations, \(\vec\nabla f=\lambda\vec\nabla g\), are \[ y=\dfrac{\lambda x}{9} \qquad x=\dfrac{\lambda y}{4} \] Solving for \(\lambda\) in each equation yields \[ \lambda = \dfrac{9y}{x} = \dfrac{4x}{y} \implies x^2=\dfrac{9y^2}{4} \qquad \text{(*)} \] Plugging this result into the constraint equation gives: \[\begin{aligned} \dfrac{1}{18}\dfrac{9y^2}{4} + \dfrac{y^2}{8}&=1 \\ \dfrac{y^2}{8} + \dfrac{y^2}{8}&=1 \\ y^2 &= 4 \\ y &= \pm 2 \end{aligned}\] Plugging these values of \(y\) back into (*) gives \(x = \pm 3\). This results in 4 critical points along the elliptical constraint: \[ (3,2) \qquad (3,-2) \qquad (-3,2) \qquad (-3,-2) \] We compute the values of \(f=xy\): \[ f(3,2)=f(-3,-2)=6 \quad \text{and} \quad f(3,-2)=f(-3,2)=-6 \] Consequently, the smallest value of \(f\) is \(-6\) and largest values is \(6\).

    wll 

20. Find the largest and smallest values of the function \(f(x,y,z)=xyz\) on the ellipsoid \(\dfrac{x^2}{18}+\dfrac{y^2}{8}+\dfrac{z^2}{2}=1\).

    In the plot, the ellipsoid is red, the level sets of \(f\) where \(f \gt 0\) are blue, and the level sets of \(f\) where \(f \lt 0\) are yellow.

    

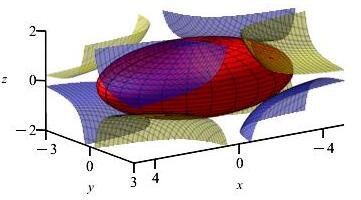
    Do the previous problem first. The solutions are similar and the proccess is identical.

    The smallest value is \(-\dfrac{4\sqrt{6}}{3}\).
    The largest value is \(\dfrac{4\sqrt{6}}{3}\).

    We maximize and minimize the function \(f=xyz\) with the constraint ellipsoid \(g = \dfrac{x^2}{18}+\dfrac{y^2}{8}+\dfrac{z^2}{2}=1\).
    
    The gradients of the functions are \[ \vec\nabla f=\langle yz,xz,xy \rangle \qquad \vec\nabla g=\left\langle \dfrac{x}{9},\dfrac{y}{4},z \right\rangle \] The Lagrange equations, \(\vec\nabla f=\lambda\vec\nabla g\), are \[ yz=\dfrac{\lambda x}{9} \qquad xz=\dfrac{\lambda y}{4} \qquad xy=\lambda z \] We multiply the first equation by \(x\), the second by \(y\) and the third by \(z\) and equate them: \[ xyz =\dfrac{\lambda x^2}{9} = \dfrac{\lambda y^2}{4} =\lambda z^2 \] These tell us: \[ x^2=9z^2 \qquad y^2=4z^2 \qquad \text{(*)} \] Plugging these equations into the constraint equation gives: \[\begin{aligned} \dfrac{9z^2}{18} + \dfrac{4z^2}{8} + \dfrac{z^2}{2} &=1 \\ \dfrac{3z^2}{2} &=1 \\ z &= \pm\,\dfrac{\sqrt{2}}{\sqrt{3}} \end{aligned}\] Plugging these values of \(z\) into (*) gives: \[\begin{aligned} x^2=9\dfrac{2}{3} &\implies x = \pm\,\sqrt{6} \\ y^2=4\dfrac{2}{3} &\implies y = \pm\,\dfrac{2\sqrt{2}}{\sqrt{3}} \end{aligned}\] Plugging positive and negative variations of \((x,y,z)=\left(\pm\,\sqrt{6},\pm\,\dfrac{2\sqrt{2}}{\sqrt{3}}, \pm\,\dfrac{\sqrt{2}}{\sqrt{3}}\right)\) into \(f=xyz\) give \(f=\pm\,\dfrac{4\sqrt{6}}{3}\). So the a minimum value of \(f\) is \(-\dfrac{4\sqrt{6}}{3}\) and the maximum value is \(\dfrac{4\sqrt{6}}{3}\).

    wll,tj 

PY: x3d plot not showing.

21. A \(425\,\text{cm}\) wire is cut into \(2\) pieces of lengths \(a\) and \(b\). The piece of length \(a\) is bent into a square. The piece of length \(b\) is bent into a rectangle whose length is twice its width. What are \(a\) and \(b\) which minimize or maximize the total area enclosed by both pieces? (Allow for the case that \(a\) or \(b\) is zero.)

    

    Express the total area as a function of its segment lengths \(a\) and \(b\). Find the critical points where \(a\) and \(b\) are both non-zero and where one is zero. Then make a table of values.

    Minimized Area \(=\dfrac{10625}{2}\approx 5312.5\)
    at \(a=200\,\text{cm}\) and \(b=225\,\text{cm}\)
    
    Maximized Area \(=\dfrac{180625}{16}\approx11289.\)
    at \(a=425\,\text{cm}\) and \(b=0\,\text{cm}\)
    
    Note: The maximized area occurs when \(a\) has all of the wire. If you think of a puddle of water on a piece of glass, it will contract into a circle which has maximum area and minimum perimeter. Here we are constrained to a square and a rectangle and the square with no rectangle is the closest thing to a circle.

    We represent the length of the original wire as a sum of its parts: \[ a + b = 425 \qquad \text{(1)} \] To minimize the total area of the shapes, we find the area of each shape as a function of the wire segment lengths. First the segment of length \(a\) is folded into a square of side \(s\): \[\begin{aligned} \text{Perimeter}_{a} &= a = 4s \quad \Rightarrow \quad s = \dfrac{a}{4}\\ \text{Area}_{a} &= s^2= \dfrac{a^2}{16} \end{aligned}\] And now the segment of length \(b\) is folded into a rectangle of width \(w\) and length \(2w\): \[\begin{aligned} \text{Perimeter}_{b} &= b = 2w + w + 2w + w = 6w \quad \Rightarrow \quad w = \dfrac{b}{6}\\ \text{Area}_{b} &= 2w \cdot w = 2w^2= \dfrac{b^2}{18} \end{aligned}\] The total area is then the sum of two areas. \[ A = \dfrac{a^2}{16} + \dfrac{b^2}{18} \qquad (*) \] We apply the constraint (1) by plugging \(b=425-a\) into our total area function: \[ A= \dfrac{a^2}{16} + \dfrac{(425-a)^2}{18} \] We set the derivative equal to \(0\) and solve of \(a\): \[\begin{aligned} &\dfrac{dA}{da} = \dfrac{a}{8} - \dfrac{425-a}{9}=0 \quad \Rightarrow \quad 9a=8(425-a) \\ &\Rightarrow \quad 17a=3400 \quad \Rightarrow \quad a= 200 \end{aligned}\] Plugging back this gives: \[ b=425-a=425-200=225 \] We test the critical points and the endpoint cases (where \(a\) or \(b\) are zero) to see which is a minimum or maximum. We plug \(a\) and \(b\) into (*) and make a table of values:

    \(a\)	\(b\)	Area	Classification
    \(200\)	\(225\)	\(\dfrac{10625}{2}\approx 5312.5\)	Local Minimum
    \(0\)	\(425\)	\(\dfrac{180625}{18}\approx10035.\)	Neither
    \(425\)	\(0\)	\(\dfrac{180625}{16}\approx11289.\)	Local Maximum

    wll,tj 

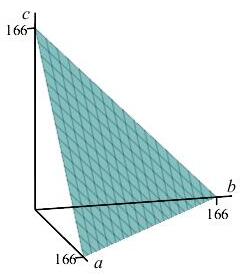
22. A \(166\,\text{cm}\) wire is cut into \(3\) pieces of lengths \(a\), \(b\) and \(c\). The piece of length \(a\) is bent into a square. The piece of length \(b\) is bent into a rectangle whose length is twice its width. The piece of length \(c\) is bent into a rectangle whose length is \(3\) times its width. What are \(a\), \(b\) and \(c\) which minimize and maximize the total area enclosed by all \(3\) pieces? (Allow for cases where \(a\), \(b\), or \(c\) are zero.)

    

    Express the total area as a function of its segment lengths \(a\), \(b\) and \(c\). Find the critical points where \(a\), \(b\) and \(c\) are all non-zero, where one is zero and where two are zero. Then make a table of values.

    Maximized Area:
    \(a = 166 \quad \) \(b = 0 \quad \) \(c = 0\)
    Minimized Area:
    \(a = 48 \quad \) \(b = 54 \quad \) \(c = 64\)
    
    Note: The maximized area occurs when \(a\) has all of the wire. If you think of a puddle of water on a piece of glass, it will contract into a circle which has maximum area and minimum perimeter. Here we are constrained to a square and two rectangles and the square with no rectangles is the closest thing to a circle.

    We express the length of the wire as the sum of its parts: \[ L(a,b,c) = a + b +c = 166 \] To minimize the total area of the shapes, we find the area of each shape as a function of the wire segment lengths.
    The piece of length \(a\) is folded into a square of side \(s\): \[\begin{aligned} \text{Perimeter}_{a} &= a = 4s \\ \text{Area}_{a} &= s^2= \dfrac{a^2}{16} \end{aligned}\] The piece of length \(b\) is folded into a rectangle of width \(w\) and length \(2w\): \[\begin{aligned} \text{Perimeter}_{b} &= b = 2w + w + 2w + w = 6w \\ \text{Area}_{b} &= 2w \cdot w = 2w^2= \dfrac{b^2}{18} \end{aligned}\] The piece of length \(3\) is folded into a rectangle of width \(W\) and length \(3W\): \[\begin{aligned} \text{Perimeter}_{c} &= c = 3W + W +3W + W = 8W \\ \text{Area}_{c} &= 3W \cdot W = 3W^2= \dfrac{3c^2}{64} \end{aligned}\] The total area is then found by adding the three areas: \[\begin{aligned} A &= \dfrac{a^2}{16} + \dfrac{b^2}{18}+ \dfrac{3c^2}{64}\\ \end{aligned}\] The gradients of the functions are \[ \vec\nabla A=\left(\dfrac{a}{8}, \dfrac{b}{9}, \dfrac{3c}{32}\right) \qquad \vec\nabla L=\left(1,1,1\right) \] The Lagrange equations, \(\vec\nabla A=\lambda\vec\nabla L\), are \[\begin{aligned} \dfrac{a}{8}&=\lambda \qquad \text{(1)} \\ \dfrac{b}{9}&=\lambda \qquad \text{(2)} \\ \dfrac{3c}{32}&=\lambda \qquad \text{(3)} \end{aligned}\] Solving for \(b\) and \(c\) in terms of \(a\) gives: \[\begin{aligned} \dfrac{a}{8}&=\dfrac{b}{9} &\implies b=\dfrac{9a}{8} \\ \dfrac{a}{8}&=\dfrac{3c}{32} &\implies c=\dfrac{4a}{3} \end{aligned}\] Plugging these results into the constraint \(L=166\) gives: \[\begin{aligned} a + \dfrac{9a}{8} + \dfrac{4a}{3} &= 166 \\ \dfrac{83a}{24} &= 166 \\ a &= 48 \end{aligned}\] And using this value in previous equations yields: \[ b = 54 \qquad c = 64 \]

    So a critical point is \(\left(48,54, 64\right)\).

    We also need to check the boundaries. The plane, \(a+b+c=166\), intersects the first quadrant in a triangle. So we check the \(3\) edges (where one of \(a\), \(b\) or \(c\) is zero and we need to extremize relative to the \(2\) other variables) and the \(3\) vertices (where two are zero and other one is \(166\)). For the edges, we compute:

    First, when \(a=0\):

    

    \[\begin{aligned} A &= \dfrac{b^2}{18}+ \dfrac{3c^2}{64} \qquad &L(b,c) &= b + c = 166\\ \vec\nabla A&=\left(\dfrac{b}{9}, \dfrac{3c}{32}\right) &\vec\nabla L&=(1,1) \end{aligned}\] The Lagrange equations and the constraint lead to: \[\begin{aligned} b &= \dfrac{27c}{32}\\ \dfrac{27c}{32} + c &= 166\\ c &= \dfrac{5312}{59} \qquad b=\dfrac{4482}{59} \end{aligned}\] Then when \(b=0\) \[\begin{aligned} f(a,b,c) &= a + c = 166\\ A &= \dfrac{a^2}{16} + \dfrac{3c^2}{64}\\ \vec\nabla A&=\left(\dfrac{a}{8}, \dfrac{3c}{32}\right)\\ a &= \dfrac{3c}{4}\\ \dfrac{3c}{4} + c &= 166\\ c &= \dfrac{664}{7} \qquad a=\dfrac{498}{7} \end{aligned}\] Then when \(c=0\) \[\begin{aligned} f(a,b,c) &= a + b = 166\\ A &= \dfrac{a^2}{16} + \dfrac{b^2}{18}\\ \vec\nabla A&=\left(\dfrac{a}{8}, \dfrac{b}{9}\right)\\ a &= \dfrac{8b}{9}\\ \dfrac{8b}{9} + b &= 66\\ b &= \dfrac{1494}{17} \qquad a=\dfrac{1328}{17} \end{aligned}\] We make a table of values:

    \(a\)	\(b\)	\(c\)	Area	Classification
    \(48\)	\(54\)	\(64\)	\(498\)	Local Minimum
    \(0\)	\(\dfrac{4482}{59}\)	\(\dfrac{5312}{59}\)	\(\dfrac{41334}{59}\approx700.6\)	Neither
    \(\dfrac{498}{7}\)	\(0\)	\(\dfrac{664}{7}\)	\(\dfrac{20667}{28}\approx738.1\)	Neither
    \(\dfrac{1328}{17}\)	\(\dfrac{1494}{17}\)	\(0\)	\(\dfrac{13778}{17}\approx810.5\)	Neither
    \(0\)	\(0\)	\(166\)	\(\dfrac{20667}{16}\approx1292.\)	Neither
    \(0\)	\(166\)	\(0\)	\(\dfrac{13778}{9}\approx1531.\)	Neither
    \(166\)	\(0\)	\(0\)	\(\dfrac{6889}{4}\approx1722.\)	Local Maximum

    wll,tj 

23. A farmer wants to fence in a grazing field and split it into two pieces for cows and horses. The field will be a rectangle surrounded by fence with a divider fence parallel to one side. What are the length and width of the field which maximize the total area if the total length of fence is \(3000\) meters?

    

    Write the area and perimeter in terms of \(x\) and \(y\). Then set up the Lagrange equations.

    The dimensions that maximize the area are:
    \(x = 750\) and \(y = 500\)
    where \(y\) is the length as the partition. These dimensions produce a total area of \(A=375000\).

    The total fence length is written as a function of width, \(x\), and the height \(y\) including the partition. So the perimeter constraint is: \[ P(x,y) = 2x+3y = 3000 \] The total enclosed area is: \[ A(x,y) = xy \] The gradients of the functions are \[ \vec\nabla A=\langle y,x \rangle \qquad \vec\nabla P=\langle 2,3 \rangle \] The Lagrange equations, \(\vec\nabla A=\lambda\vec\nabla P\), are \[\begin{aligned} y&=\lambda 2 \qquad \text{(1)} \\ x&=\lambda 3 \qquad \text{(2)} \end{aligned}\] Dividing equation (1) by equation (2) yields \(y=\dfrac{2}{3}x\).
    Plugging this into the constrained equation gives: \[\begin{aligned} 2x+3\left(\dfrac{2}{3}x\right) &= 3000 \\ 2x + 2x &= 3000 \\ x &= 750 \end{aligned}\] We plug this the formula for \(y\) to get \(y = 500\). These two dimensions produce a total area of \(A=750\cdot500=375000\).

    This area is the maximum because \(y\) is constrained to \(0 \le y \le 1000\) and the area is \(0\) at both endpoints while the only interior critical point gives a positive area.

    wll,tj 

24. A box manufacturer wants to make a rectangular solid cardboard box with a vertical cardboard divider which splits the interior into \(2\) compartments, each containing \(12\,000\,\text{cm}^3\). Because of folding, the top and bottom will have \(2\) layers of cardboard. What are the dimensions of the box which uses the least amount of cardboard?

    

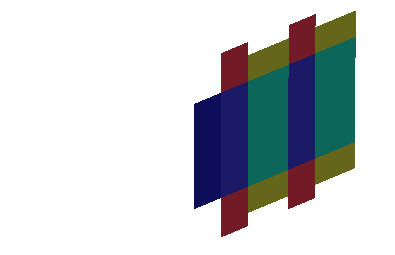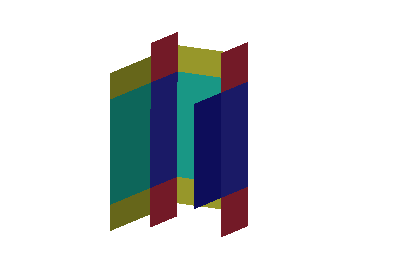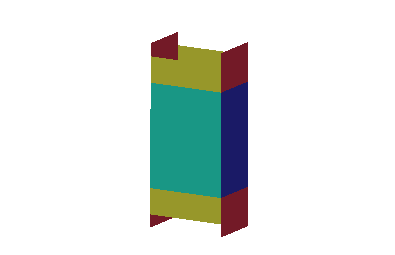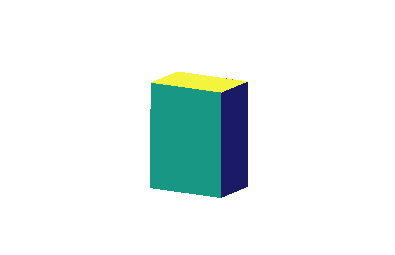
    Express the volume and surface area in terms of the box's length, width and height. Be sure to include the area of the partition. The volume is the constraint. Minimize the surface area.

    \( x=30\,\text{cm} \quad y=20\,\text{cm} \quad z=40\,\text{cm} \)

    Let \(x\) and \(y\) be the length and width of the box and let \(z\) be the height. There are \(4\) layers of cardboard on the top and bottom with area \(xy\). There are \(2\) layers of cardboard in the front and back with area \(xz\). Finally, there are \(3\) layers of cardboard on the left, the right and the partition with area \(yz\). All together, the area is: \[ A(x, y, z) = 4xy + 2xz + 3yz \] And the total enclosed volume is: \[ V(x,y,z) = xyz = 2\cdot12\,000 = 24\,000 \] The gradients of the functions are \[ \vec\nabla A=\langle 4y+2z,4x+3z,2x+3y \rangle \qquad \vec\nabla V=\langle yz,xz,xy \rangle \] The Lagrange equations, \(\vec\nabla A=\lambda\vec\nabla V\), are \[\begin{aligned} 4y+2z&=\lambda yz \qquad \text{(1)} \\ 4x+3z&=\lambda xz \qquad \text{(2)} \\ 2x+3yx&=\lambda xy \qquad \text{(3)} \end{aligned}\] We multiply equation (1) by \(x\), equation (2) by \(y\), and equation (3) by \(z\). We then equate and solve: \[\begin{aligned} \lambda xyz&=2xz+4xy = 3yz+4xy = 3yz+2xz \\ &\implies \quad 2x = 3y \qquad 4y = 2z \end{aligned}\] Substituting these values of \(x\) and \(z\) into the volume constraint gives: \[\begin{aligned} V &= xyz = \left(\dfrac{3y}{2}\right) y (2y) \\ &= 3y^3=24\,000 \\ \end{aligned}\] So \(y=20\,\text{cm}\), and then \(x=30\,\text{cm}\) and \(z=40\,\text{cm}\).

    wll 

25. Find the maximum value of \(f=xy\) on the line \(x+y=6\).

    

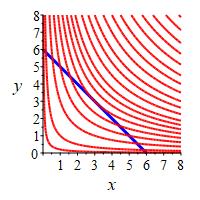
    To see the critical point \((x,y)=(a,b)\) produces a maximum, look at the values of \(f\) at the nearby point \(x=a+\delta\) and \(y=b-\delta\).

    The maximum value of \(f\) is \(f(3,3)=9\).

    We maximize \(f=xy\) with the constraint set \(g=x+y=6\). The gradients of the functions are \[ \vec\nabla f=\langle y,x \rangle \quad \text{and} \quad \vec\nabla g=\langle 1,1 \rangle \]

    

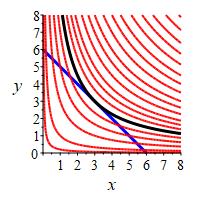
    The Lagrange equations, \(\vec\nabla f=\lambda\vec\nabla g\), are \[\begin{aligned} y = \lambda \qquad x = \lambda \quad \implies \quad x=y \end{aligned}\] Plugging this into the constraint equation gives: \[\begin{aligned} x + x &= 6 \\ x &= 3 \quad \implies \quad y=3 \end{aligned}\] So the critical point is \((x,y)=(3,3)\) where \(f(3,3)=9\). To see this is a maximum, we look at a near by point with \(x=3+\delta\) and \( y=3-\delta\). Then: \[ f(x,y)=(3+\delta)(3-\delta)=9-\delta^2 \lt 9 \] So the maximum point of \(f\) on the line \(g\) is \(f(3,3)=9\).

    wll,tj 

26. Find the minimum value of \(f=x+y\) on the branch of the hyperbola \(xy=9\) in the first quadrant. Discuss the geometrical relation between this problem and the previous problem where the constraint and the extremal are interchanged.

    

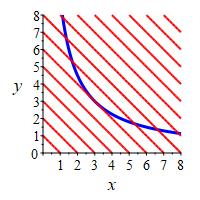
    To check the critical point is a minimum, look at the values of \(f\) at the largest and smallest value of \(x\) that are allowed.

    The minimum value of \(f\) is \(f(3, 3)=6\). The relationship is discussed in the remark.

    We minimize\(f=x+y\) with the constraint set \(g=xy=9\). The gradients of the functions are \[ \vec\nabla f=\langle 1,1 \rangle \quad \text{and} \quad \vec\nabla g=\langle y,x \rangle \]

    

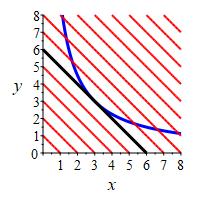
    The Lagrange equations, \(\vec\nabla f=\lambda\vec\nabla g\), are \[\begin{aligned} 1 = \lambda y \qquad 1 = \lambda x \quad \implies \quad x=y \end{aligned}\] Plugging this into the constraint equation gives: \[\begin{aligned} x^2 &= 9 \\ x &= \pm 3 \quad \implies \quad y=x=\pm3 \end{aligned}\] Since we want the point in the first quadrant, the critical points is \((3, 3)\). To see this is a minimum, we notice that when \(x\) is very large, then \(y=\dfrac{9}{x}\) is close to \(0\) and \(f(x,y)\) is very large. Similarly, when \(x\) is close to \(0\), then \(y=\dfrac{9}{x}\) is very large and \(f(x,y)\) is also very large. So there must be a minimum in between and \((3, 3)\) is the only critical point. So, the minimum point of \(f\) on the hyperbola \(g\) is \(f(3,3)=6\).

    wll,tj 

    This and the previous problem are geometricaly dual in their solution. In both scenarios, the solution (minimum or maximum) is the point of tangency of a line and a hyperbola.

    For example, the constraint \(xy=9\) of this problem is a specific hyperbola. The level sets of the extremal function \(f=x+y\) are the family of all lines with slope \(m=-1\). The solution of this problem is the point where one of these lines is tangent to the hyperbola \(xy=9\).

    Similarly, in the previous problem, the constraint \(x + y = 6\) is a specific line. The level sets of the extremal function \(f=xy\) are the family of all hyperbolas of the form \(y=\dfrac{C}{x}\). The solution of that problem is the point where one of these hyperbolas is tangnet to the line \(x+y=6\).

    The differ because the constraint and the extremal are interchanged.

27. Find the maximum volume of an cylindrical aluminum can with lids whose surface area is \(216\pi\,\text{cm}^2\).

    

    Construct functions for the volume and surface area of the can. Remember the area of the two ends. Treat \(r\) and \(h\) as you would \(x\) and \(y\).

    A radius \(r=6\) and height \(h=12\) produces a maximized volume of \(V=432\pi\).

    The curved part of the can has area \(2\pi rh\) while the top and bottom have area \(\pi r^2\). So we want the total area to be \(A=2\pi rh+2\pi r^2=216\pi\). We maximize the volume function, \(V=\pi r^2 h\) subject to the area constraint. The gradients of the functions are \[\begin{aligned} \vec\nabla V&=\langle 2\pi rh,\pi r^2 \rangle \\ \vec\nabla A&=\langle 2\pi h + 4\pi r, 2\pi r \rangle \end{aligned}\] The Lagrange equations, \(\vec\nabla V=\lambda\vec\nabla A\), are \[\begin{aligned} 2\pi rh&=\lambda (2\pi h + 4\pi r) \qquad &\text{(1)} \\ \pi r^2&=\lambda 2\pi r \qquad &\text{(2)} \end{aligned}\] Dividing equation (1) by equation (2) gives: \[\begin{aligned} \dfrac{2h}{r}&=\dfrac{h}{r}+2 \\ 2h&=h+2r \\ h &= 2r \end{aligned}\] Substituting this into the area constraint gives \[\begin{aligned} 2 \pi r^2 + 2 \pi r(2r)&=216\pi \\ 6\pi r^2&=216\pi\\ r&=6 \end{aligned}\] Therefore the critical point \(r=6\) , \(h=12\) produces a maximized volume of \(V=432\pi\).

    wll,tj 

28. Find the minimum surface area of a cylindrical aluminum can with lids whose volume is \(432\pi\,\text{cm}^3\). Discuss the geometrical relation between this problem and the previous problem.

    

    Construct functions for the volume and surface area of the can. Remember the area of the two ends. Treat \(r\) and \(h\) as you would \(x\) and \(y\).

    The radius \(r=6\) and height \(h=12\) produces a minimized surface area \(A=216\pi\).

    We minimize the surface area function, \(A= 2 \pi rh+2 \pi r^2\) , with the constraint of a fixed volume, \(V=\pi r^2 h=432\pi\).
    The gradients of the functions are \[\begin{aligned} \vec\nabla A&=\langle 2\pi h+4\pi r, 2\pi r \rangle \\ \vec\nabla V&=\langle 2\pi rh,\pi r^2 \rangle \end{aligned}\] The Lagrange equations, \(\vec\nabla A=\lambda\vec\nabla V\), are \[\begin{aligned} 2\pi h+4\pi r&=\lambda (2\pi rh) \qquad &\text{(1)} \\ 2\pi r&=\lambda(\pi r^2) \qquad &\text{(2)} \end{aligned}\] Dividing equation (1) by equation (2) gives: \[\begin{aligned} \dfrac{h}{r}+2&= \dfrac{2h}{r} \\ 2r + h&=2h \\ h &= 2r \end{aligned}\] Substituting this into the volume constraint gives \[\begin{aligned} \pi r^2 (2r)&=432\pi \\ 2\pi r^3&=432\pi\\ r&=6 \end{aligned}\] Therefore the critical point \(r=6\), \(h=12\) produces a minimized surface area \(A=216\pi\).

    wll,tj 

    This and the previous problem are geometricaly dual in their solution. In both scenarios, the solution (minimum or maximum) is the point of tangency of two curves.

    In this problem, the constraint is the specific curve \(\pi r^2 h=432\pi\). The level sets of the extremal function \(A=2 \pi rh+2 \pi r^2\) are a family of curves. The solution of this problem is the point where one of the extremal family of curves is tangent to the constraint curve.

    Similarly, in the previous problem, the constraint is the specific curve \(2 \pi rh+2 \pi r^2=216\). The level sets of the extremal function \(V=\pi r^2 h\) are a family of curves. The solution of that problem is the point where one of the extremal family of curves is tangnet to the constraint curve.

    The differ because the constraint and the extremal are interchanged.

29. Find the point(s) on the curve \(x^2y=2\) closest to the origin and give the distance from the origin.

    

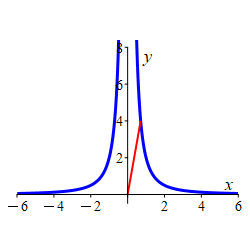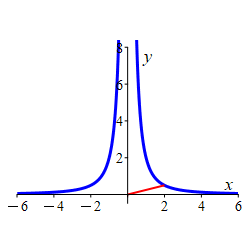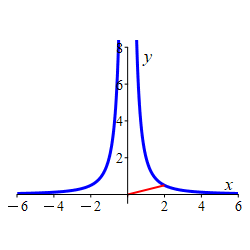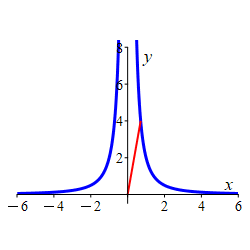
    Minimize the square of the distance instead of the distance.

    The two points closest to the origin are: \[ (\sqrt{2}, 1) \qquad \quad (-\sqrt{2}, 1) \] which are at a distance of \(D=\sqrt{3}\) from the origin.

    We minimize the square of the distance function from the origin using \(f=D^2 = x^2+y^2\) on the constraint curve \(g= x^2y=2\). The gradients of the functions are \[\begin{aligned} \vec\nabla f&=\langle 2x, 2y \rangle \\ \vec\nabla g&=\langle 2xy,x^2 \rangle \end{aligned}\] The Lagrange equations, \(\vec\nabla f=\lambda\vec\nabla g\), are \[\begin{aligned} 2x&=2\lambda xy \qquad &\text{(1)} \\ 2y&=\lambda x^2 \qquad &\text{(2)} \end{aligned}\] We divide (1) by (2) giving \(\dfrac{x}{y}=\dfrac{2y}{x}\) or \(x^2=2y^2\). Plugging this into the constraint \(x^2y=2\) yields: \[\begin{aligned} 2y^3&=2 \\ y &= 1 \\ x&=\pm\sqrt{2} \end{aligned}\] So the two minima points are: \[ (\sqrt{2}, 1) \qquad \quad (-\sqrt{2}, 1) \] which are at a distance \(D=\sqrt{\sqrt{2}^2+1^2}=\sqrt{3}\) from the origin.

    wll,tj 

30. Find the point on the surface \(x^4y^2z=32\) closest to the origin.

    

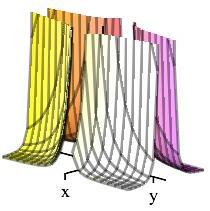
    Minimize the square of the distance instead of the distance.

    The four points closest to the origin are: \[ (\pm2, \pm\sqrt{2}, 1) \] which are at a distance of \(D=\sqrt{7}\) from the origin.

    We minimize the square of the distance function from the origin using \(f=D^2 = x^2+y^2+z^2\) on the constraint curve \(g= x^4y^2z=32\). The gradients of the functions are \[\begin{aligned} \vec\nabla f&=\langle 2x, 2y, 2z \rangle \\ \vec\nabla g&=\langle 4x^3y^2z,2x^4yz,x^4y^2 \rangle \end{aligned}\] The Lagrange equations, \(\vec\nabla f=\lambda\vec\nabla g\), are \[\begin{aligned} 2x&=4\lambda x^3y^2z \qquad &\text{(1)} \\ 2y&=2\lambda x^4yz \qquad &\text{(2)}\\ 2z&=\lambda x^4y^2 \qquad &\text{(3)} \end{aligned}\] We divide (1) by (3) giving \(\dfrac{x}{z}=\dfrac{4z}{x}\) or \(x^2=4z^2\). We also divide (2) by (3) giving \(\dfrac{y}{z}=\dfrac{2z}{y}\) or \(y^2=2z^2\). Plugging this into the constraint \(x^4y^2z=32\) yields: \[\begin{aligned} (16z^4)(2z^2)(z)&=32 \\ 32z^7&=32 \\ z &=1 \\ x &=\pm2 \\ y &= \pm \sqrt{2} \end{aligned}\] So the the \(4\) minima points are: \[ (\pm2, \pm\sqrt{2}, 1) \] which are at a distance \(D=\sqrt{2^2+\sqrt{2}^2+1^2}=\sqrt{7}\) from the origin.

    wll,tj 

31. Find the volume of the largest rectangular solid with \(3\) faces in the coordinate planes and the opposite vertex on the plane \(\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1\) where \(a \ge 0\), \(b \ge 0\) and \(c \ge 0\).

    

    Write the volume of the solid described in the question as a function of \(x\), \(y\), and \(z\) Then you can use Lagrange equations to solve for the maximized volume.

    The maximized volume has a value of: \(V=\dfrac{abc}{27}\)

    We maximize the volume, \(V=xyz\) where \((x,y,z)\) is the vertex on the plane \(g=\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1\). The gradients of the functions are \[\begin{aligned} \vec\nabla V&=\left\langle yz, xz, xy\right\rangle \\ \vec\nabla g&=\left\langle\dfrac{1}{a},\dfrac{1}{b},\dfrac{1}{c}\right\rangle \end{aligned}\] The Lagrange equations, \(\vec\nabla V=\lambda\vec\nabla g\), are \[\begin{aligned} yz&=\dfrac{\lambda}{a} \qquad &\text{(1)} \\ xz&=\dfrac{\lambda}{b} \qquad &\text{(2)}\\ xy&=\dfrac{\lambda}{c} \qquad &\text{(3)} \end{aligned}\] We equate lambda in each equation, which yields the following equations: \[\begin{aligned} ayz=bxz=cxy \implies x=\dfrac{ay}{b} \quad \text{and} \quad z=\dfrac{cy}{b} \end{aligned}\] Substituting these values into the equation of the plane produces: \[\begin{aligned} \dfrac{\;\dfrac{ay}{b}\;}{a}+\dfrac{y}{b}+\dfrac{\;\dfrac{cy}{b}\;}{c}&=1 \\ \dfrac{y}{b}+\dfrac{y}{b}+\dfrac{y}{b}&=1 \\ y &= \dfrac{b}{3} \end{aligned}\] We use this value to solve for \(x\) and \(z\). \[\begin{aligned} x=\dfrac{a\left(\dfrac{b}{3}\right)}{b} \implies x=\dfrac{a}{3} \\ z=\dfrac{c\left(\dfrac{b}{3}\right)}{b} \implies z=\dfrac{c}{3} \end{aligned}\] So the critical point is: \[\begin{aligned} \left(\dfrac{a}{3},\dfrac{b}{3},\dfrac{c}{3}\right) \end{aligned}\] With a corresponding maximized volume of \[ V=\dfrac{a}{3} \cdot \dfrac{b}{3} \cdot \dfrac{c}{3} =\dfrac{abc}{27} \]

    wll,tj 

32. We would like to find the line \(y=f(x)=mx+b\) which best fits a collection of \(20\) data points \[ (x_1,y_1), \quad (x_2,y_2), \quad \cdots, \quad (x_{20},y_{20}) \] using a quadratic fit. For each point, \((x_i,y_i)\), the vertical distance to the line is \(|y_i-f(x_i)|\). Click here to toggle the vertical line segments whose lengths are \(|y_i-f(x_i)|\). To say we want a quadratic fit, means we want to find \(m\) and \(b\) so that the sum of the squared vertical distances \[ S=\sum_{i=1}^{20} \left(y_i-f(x_i)\right)^2 \] is a minimum. Find formulas for \(m\) and \(b\) in terms of the \(x_i\)'s and \(y_i\)'s. What happens if we have more than \(20\) points?

    

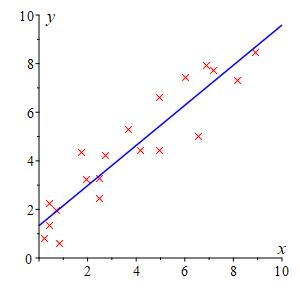
    Note: The \(x_i\)'s and \(y_i\)'s are constants. The variables are \(m\) and \(b\). It may help to start with fewer points, say \(3\), so you can write out all the terms in the summation.

    For 20 samples, the formula for \(m\) and \(b\) are: \[\begin{aligned} m&=\dfrac{\displaystyle 20\sum_{i=1}^{20}x_i y_i-\sum_{i=1}^{20}x_i\sum_{i=1}^{20}y_i} {\displaystyle 20\sum_{i=1}^{20} x_i^2 - \left(\sum_{i=1}^{20} x_i\right)^2} \\ b&=\dfrac{\displaystyle \sum_{i=1}^{20}y_i\sum_{i=1}^{20}x_i^2-\sum_{i=1}^{20}x_i\sum_{i=1}^{20}x_i y_i} {\displaystyle 20\sum_{i=1}^{20} x_i^2 - \left(\sum_{i=1}^{20} x_i\right)^2} \end{aligned}\] General Formula: \[\begin{aligned} m&=\dfrac{\displaystyle n\sum_{i=1}^{n}x_i y_i-\sum_{i=1}^{n}x_i\sum_{i=1}^{n}y_i} {\displaystyle n\sum_{i=1}^{n} x_i^2 - \left(\sum_{i=1}^{n} x_i\right)^2} \\ b&=\dfrac{\displaystyle \sum_{i=1}^{n}y_i\sum_{i=1}^{n}x_i^2-\sum_{i=1}^{n}x_i\sum_{i=1}^{n}x_i y_i} {\displaystyle n\sum_{i=1}^{n} x_i^2 - \left(\sum_{i=1}^{n} x_i\right)^2} \end{aligned}\]

    We treat \(S\) as a function, \(S(m,b)\), where \(x_{i}\) and \(y_{i}\) are constants. We substitute \(f(x_i)\): \[\begin{aligned} S&=\sum_{i=1}^{20} \left(y_i-(mx_i+b)\right)^2 \\ &=\sum_{i=1}^{20} \left(y_i-mx_i-b\right)^2 \end{aligned}\] We take the partial derivatives with respect to \(m\): \[\begin{aligned} S_m&=\sum_{i=1}^{20} 2\left(y_i-mx_i-b\right)(-x_i) \\ &= 2m\sum_{i=1}^{20} x_i^2+ 2b\sum_{i=1}^{20}x_i -2\sum_{i=1}^{20}x_i y_i \end{aligned}\] and with respect to \(b\): \[\begin{aligned} S_b&=\sum_{i=1}^{20} 2\left(y_i-mx_i-b\right)(-1) \\ &=2m\sum_{i=1}^{20} x_i + 40b -2\sum_{i=1}^{20}y_i \end{aligned}\] To simplify the computation, we introduce the notation: \[ \Sigma_x=\sum_{i=1}^{20} x_i \quad \Sigma_y=\sum_{i=1}^{20} y_i \quad \Sigma_{xx}=\sum_{i=1}^{20} x_i^2 \quad \Sigma_{xy}=\sum_{i=1}^{20}x_i y_i \] To minimize \(S(m,b)\) we set (half) the partial derivatives equal to \(0\): \[\begin{aligned} \dfrac{1}{2}S_m &= m \Sigma_{xx} + b\Sigma_x -\Sigma_{xy}=0 \qquad &\text{(1)} \\ \dfrac{1}{2}S_b &= m\Sigma_x + 20b -\Sigma_y=0 \qquad &\text{(2)} \end{aligned}\] And we solve this system of linear equations for \(m\) and \(b\). Solving equation (2) for \(b\) gives: \[\begin{aligned} b &=\dfrac{1}{20}\Sigma_y - \dfrac{m}{20}\Sigma_x \end{aligned}\] Plugging this value of \(b\) into equation (1) gives: \[\begin{aligned} m\Sigma_{xx}+ \left(\dfrac{1}{20}\Sigma_y - \dfrac{m}{20}\Sigma_x\right)\Sigma_x -\Sigma_{xy}&=0 \\ 20m\Sigma_{xx}+\Sigma_x\Sigma_y -m{\Sigma_x}^2 -20\Sigma_{xy}&=0 \\ \end{aligned}\] We solve for \(m\): \[\begin{aligned} m\left(20\Sigma_{xx}-{\Sigma_x}^2\right) &=20\Sigma_{xy}-\Sigma_x\Sigma_y\\ m&=\dfrac{20\Sigma_{xy}-\Sigma_x\Sigma_y}{20\Sigma_{xx}-{\Sigma_x}^2} \end{aligned}\] And plugging this value of \(m\) back into the solution for \(b\) gives: \[\begin{aligned} b &=\dfrac{\Sigma_y}{20}-\dfrac{\Sigma_x}{20} \left(\dfrac{20\Sigma_{xy}-\Sigma_x\Sigma_y} {20\Sigma_{xx}-{\Sigma_x}^2}\right)\\ &=\dfrac{20\Sigma_y\Sigma_{xx}-\Sigma_y{\Sigma_x}^2-20\Sigma_x\Sigma_{xy}+{\Sigma_x}^2\Sigma_y} {20(20\Sigma_{xx}-{\Sigma_x}^2)} \\ &=\dfrac{20\Sigma_y\Sigma_{xx}-20\Sigma_x\Sigma_{xy}} {20(20\Sigma_{xx}-{\Sigma_x}^2)} \\ &=\dfrac{\Sigma_y\Sigma_{xx}-\Sigma_x\Sigma_{xy}} {20\Sigma_{xx}-{\Sigma_x}^2} \end{aligned}\] This produces the final solutions: \[ m=\dfrac{20\Sigma_{xy}-\Sigma_x\Sigma_y}{20\Sigma_{xx}-{\Sigma_x}^2} \qquad\qquad b=\dfrac{\Sigma_y\Sigma_{xx}-\Sigma_x\Sigma_{xy}}{20\Sigma_{xx}-{\Sigma_x}^2} \]

    ---

    General formulas are found by repeating the process with \(n\) rather than \(20\). \[ m=\dfrac{n\Sigma_{xy}-\Sigma_x\Sigma_y}{n\Sigma_{xx}-{\Sigma_x}^2} \qquad\qquad b=\dfrac{\Sigma_y\Sigma_{xx}-\Sigma_x\Sigma_{xy}}{n\Sigma_{xx}-{\Sigma_x}^2} \] where \[ \Sigma_x=\sum_{i=1}^n x_i \quad \Sigma_y=\sum_{i=1}^n y_i \quad \Sigma_{xx}=\sum_{i=1}^n x_i^2 \quad \Sigma_{xy}=\sum_{i=1}^n x_i y_i \]

    wll,tj 

33. Find the locations and values of the global maximum and minimum of the function \(f(x,y)=3x+4y\) on the circle \(x^2+y^2=1\).

    In the plot, the circle is red and the level sets of \(f\) are blue.

    

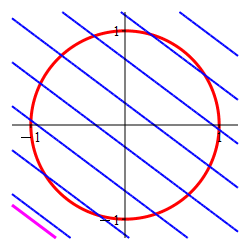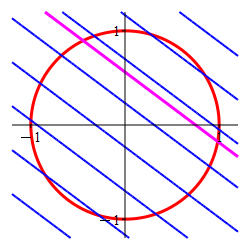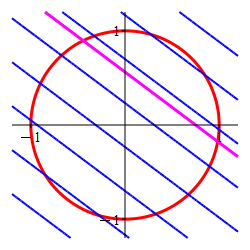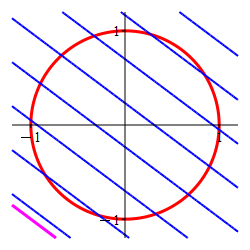
    1. Solve using a Lagrange multiplier.

       Find all the critical points on the circle, then make a table of values to determine the minimum and maximum locations.

       Global Maximum: \[ f=5 \quad \text{at} \quad (x,y)=\left(\dfrac{3}{5},\dfrac{4}{5}\right) \] Global Minimum: \[ f=-5 \quad \text{at} \quad (x,y)=\left(-\,\dfrac{3}{5},-\,\dfrac{4}{5}\right) \]

       We check for critical points on the boundary circle using the Lagrange method. The gradients of the functions are \[\begin{aligned} \vec\nabla f &=\langle 3,4 \rangle \\ \vec\nabla g &=\langle 2x,2y \rangle \end{aligned}\] The Lagrange equations, \(\vec\nabla f=\lambda\vec\nabla g\), are \[\begin{aligned} 3 = 2\lambda x \qquad \text{(1)}\\ 4 = 2\lambda y \qquad \text{(2)} \end{aligned}\] We divide equation (1) by equation (2) to get \(\dfrac{3}{4}=\dfrac{x}{y}\) which implies \(x=\dfrac{3}{4}y\). We plug this into the contraint \(g=x^2+y^2=1\) \[\begin{aligned} \left(\dfrac{3y}{4}\right)^2+y^2&=1 \\ y^2&=\dfrac{16}{25} \\ y&=\pm \dfrac{4}{5} \end{aligned}\] We use this value to solve for \(x\): (Note they must have the same sign.) \[\begin{aligned} x=\dfrac{3\left(\pm \dfrac{4}{5}\right)}{4} \implies x=\pm \dfrac{3}{5} \end{aligned}\] So our critical points are: \[\begin{aligned} \left(\dfrac{3}{5}, \dfrac{4}{5}\right) \qquad \text{and} \qquad \left(-\,\dfrac{3}{5}, -\,\dfrac{4}{5}\right) \end{aligned}\] We make a table of values:

       \(x\)	\(y\)	\(f\)
       \(\dfrac{3}{5}\)	\(\dfrac{4}{5}\)	\(5\)
       \(-\dfrac{3}{5}\)	\(-\dfrac{4}{5}\)	\(-5\)

       So the global maximum is \(f=5\) at \((x,y)=\left(\dfrac{3}{5},\dfrac{4}{5}\right)\) and the global minimum is \(f=-5\) at \((x,y)=\left(-\,\dfrac{3}{5},-\,\dfrac{4}{5}\right)\).

       wll, tj 

       The Lagrange multiplier method is designed to find the point where a level set of the optimal function is tangent to the constraint set. Here the constraint is the circle (in red) and the level sets of the optimal function are the straignt lines, (in blue) which are tangent precisely at
       the maximum \((x,y)=(.6,.8)\) and
       the minimum \((x,y)=(-.6,-.8)\).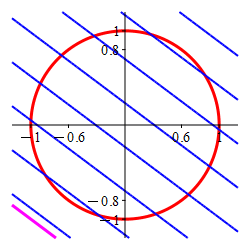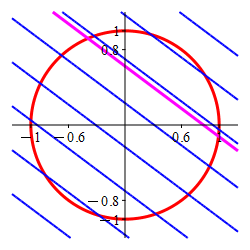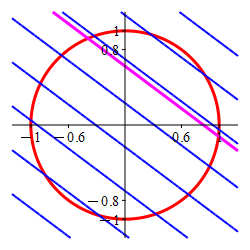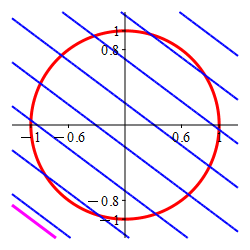

       

    2. Solve by parametrizing the constraint.

       Parametrize the circle as \((x,y)=(\cos\theta,\sin\theta)\).

       Global Maximum: \[ f=5 \quad \text{at} \quad (x,y)=\left(\dfrac{3}{5},\dfrac{4}{5}\right) \] Global Minimum: \[ f=-5 \quad \text{at} \quad (x,y)=\left(-\,\dfrac{3}{5},-\,\dfrac{4}{5}\right) \]

       We parametrize the circle as \((x,y)=(\cos\theta,\sin\theta)\). Then the extremal function becomes: \[\begin{aligned} f&=3x+4y \\ &=3\cos\theta+4\sin\theta \\ \end{aligned}\] We set the derivative equal to \(0\) and solve for \(\theta\): \[\begin{aligned} f'(\theta)=-3\sin\theta&+4\cos\theta=0 \\ \tan\theta&=4/3 \end{aligned}\] Since the tangent is positive, the angle must be in the \(1^\text{st}\) or \(3^\text{rd}\) quadrants. So the solutions are: \[\begin{aligned} \cos\theta_1&=\dfrac{3}{5} &\sin\theta_1&=\dfrac{4}{5} &(x_1,y_1)&=\left(\dfrac{3}{5},\dfrac{4}{5}\right) \\ \cos\theta_2&=-\,\dfrac{3}{5} &\sin\theta_2&=-\,\dfrac{4}{5} &(x_2,y_2)&=\left(-\,\dfrac{3}{5},-\,\dfrac{4}{5}\right) \end{aligned}\] Finally, we evaluate the extremal at the points: \[\begin{aligned} f(x_1,y_1) &=3\cdot\dfrac{3}{5}+4\cdot\dfrac{4}{5} \\ &=\dfrac{9}{5}+\dfrac{16}{5} =\dfrac{25}{5}=5 \\ f(x_2,y_2) &=3\cdot\dfrac{-3}{5}+4\cdot\dfrac{-4}{5} \\ &=-\dfrac{9}{5}-\dfrac{16}{5} =-\dfrac{25}{5}=-5 \end{aligned}\] So the global maximum is \(f\left(\dfrac{3}{5},\dfrac{4}{5}\right)=5\) and the global minimum is \(f\left(-\,\dfrac{3}{5},-\,\dfrac{4}{5}\right)=-5\).

       tj 

34. An aquarium is to have a volume of \(1620\,\text{cm}^3\). Its base will be made of marble which costs $\(.50\) per \(\text{cm}^2\). The front will be glass which costs $\(.10\) per \(\text{cm}^2\). The sides and back will be aluminum which costs $\(.05\) per \(\text{cm}^2\). What are the dimensions of the cheapest such aquarium?

    

    Construct two functions, the cost of the aquarium (optimizing), and the volume of the aquarium (constraint) as functions of the dimensions.

    The cheapest dimensions of the aquarium are (length) \(x = 6\,\text{cm}\), (depth) \(y = 9\,\text{cm}\), and (height) \(z=30\,\text{cm}\)

    We define \(x\),\(y\), and \(z\) such that the area of the base is \(xy\), the front is \(xz\), and the sides are \(yz\). We then create a function for the cost of the aquarium: \[\begin{aligned} C &= (.5)xy + (.1)xz + 2(.05)yz + (.05)xz \\ C &= .5xy + .15xz + .1yz \end{aligned}\] With the defined contraint volume of \(V = xyz = 1620\), we minimize \(C\) with contraint \(V\) using the Lagrange method. The gradients of the functions are \[\begin{aligned} \vec\nabla C &=\langle .5y + .15z,.5x + .1z, .15x + .1y \rangle \\ \vec\nabla V &=\langle yz,xz,xy \rangle \end{aligned}\] The Lagrange equations, \(\vec\nabla C=\lambda\vec\nabla V\), are \[\begin{aligned} .5y + .15z = \lambda yz \qquad \text{(1)}\\ .5x + .1z = \lambda xz \qquad \text{(2)}\\ .15x + .1y = \lambda xy \qquad \text{(3)} \end{aligned}\] We multiply equation (1) by \(x\), equation (2) by \(y\), and equation (3) by \(z\). We can then equate the left side of each equation: \[ \lambda xyz=.5xy + .15xz = .5xy + .1yz = .15xz + .1yz \] We solve the first and second equations: \[\begin{aligned} .5xy + .15xz = .5xy + .1yz &\implies x = \dfrac{2}{3}y \\ .5xy + .1yz = .15xz + .1yz &\implies z= \dfrac{10}{3}y \end{aligned}\] Plugging these solutions for \(x\) and \(z\) into \(V\) gives: \[\begin{aligned} \left(\dfrac{2}{3}y\right)(y)\left(\dfrac{10}{3}y\right) &= 1620\\ y^3&=729 \\ y&=9 \end{aligned}\] Using this solution of \(y\) yields \(x=6\) and \(z=30\). Therefore the cheapest dimensions of the aquarium are \((6,9,30)\)

    wll,tj 

c. Global Max-Min Problems

1

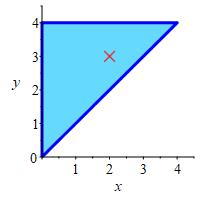
35. Find the locations and values of the global maximum and minimum of the function \(f(x,y)=2x^2-8x+y^2-6y\) inside or on the triangle with vertices \((0,0)\), \((0,4)\) and \((4,4)\).

    

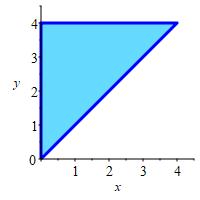
    Find the critical points in the interior, the edges, and the verticies. Then compare the values at those points to determine the minimum and maximum of the function.

    The minimum of the function in the traingular region is \(f=-17\) at \((2,3)\), and the maximum is \(f=0\) at \((0,0)\)

    To find the critical points inside the triangle, we set the partial derivatives of \(f=2x^2-8x+y^2-6y\) equal to \(0\) and solve: \[\begin{aligned} f_x = 4x - 8 = 0 \qquad \implies x = 2\\ f_y = 2y-6 = 0 \qquad \implies y=3 \end{aligned}\] From the plot, we see the critical point \((2,3)\) lies within the traingle.

    

    Next, we find all the critical points along the edges of the triangle region, represented by \(x=0\), \(y=4\), and \(y=x\). We set the partial derivatives equal to zero with each respective constraint. For \(x=0\): \[\begin{aligned} f &= y^2 - 6y \\ f_y &= 2y-6 &= 0 \qquad \implies y=3 \end{aligned}\] This implies that \((0,3)\) is a critical point on \(x=0\). Next, for \(y=4\): \[\begin{aligned} f &= 2x^2-8x-8\\ f_x &= 4x - 8 &= 0 \qquad \implies x=2 \end{aligned}\] This implies that \((2,4)\) is a critical point on \(y=4\). Next, for \(y=x\): \[\begin{aligned} f &= 2x^2-8x + x^2 - 6x = 3x^2-14x \\ f_x &= 6x-14 &= 0 \qquad \implies x=\dfrac{7}{3} \end{aligned}\] This implies that \(\left(\dfrac{7}{3}, \dfrac{7}{3}\right)\) is a critical point on \(y=x\).

    We make a table of values of \(f\) for each critical point inside, on the edges and at each vertex.

    \(x\)	\(y\)	\(f\)
    \(2\)	\(3\)	\(-17\)
    \(0\)	\(3\)	\(-9\)
    \(2\)	\(4\)	\(-16\)
    \(\dfrac{7}{3}\)	\(\dfrac{7}{3}\)	\(-\,\dfrac49{3}\approx -16.3\)
    \(0\)	\(0\)	\(0\)
    \(0\)	\(4\)	\(-8\)
    \(4\)	\(4\)	\(-8\)

    So from the table we can conclude that the minimum of the function in the traingular region is \(f=-17\) at \((2,3)\), and the maximum is \(f=0\) at \((0,0)\)

    wll 

36. Find the locations and values of the global maximum and minimum of the function \(f(x,y)=x^2+2y^2-6x-8y\) inside or on the rectangle with vertices \((0,0)\), \((4,0)\), \((4,3)\) and \((0,3)\).

    Find the critical points in the interior, the edges, and the vertices. Then compare the values at those points to determine the minimum and maximum of the function.

    The minimum is \(f=-17\) at \((3,2)\).
    The maximum is \(f=0\) at \((0,0)\).

    To find the critical points inside the rectangle, we set the partial derivatives of \(f=x^2+2y^2-6x-8y\) equal to \(0\) and solve: \[\begin{aligned} f_x = 2x - 6 = 0 \qquad \implies x = 3\\ f_y = 4y-8 = 0 \qquad \implies y=2 \end{aligned}\] The critical point \((3,2)\) lies within the rectangle \(0 \le x \le 4\) and \(0 \le y \le 3\).

    Next, we find all the critical points along the edges of the rectangle, which are \(x=0\), \(x=4\), \(y=0\), and \(y=3\). We restrict the function to each edge and then set the derivative equal to zero and solve.
    For \(x=0\): \[\begin{aligned} f &= 2y^2-8y\\ f_y &= 4y-8 &= 0 \qquad \implies (x,y)=(0,2) \end{aligned}\] For \(y=0\): \[\begin{aligned} f &= x^2-6x\\ f_x &= 2x - 6 &= 0 \qquad \implies (x,y)=(3,0) \end{aligned}\] For \(x=4\): \[\begin{aligned} f &= (4)^2+2y^2-6(4)-8y = 2y^2-8y-8\\ f_y &= 4y-8 = 0 \qquad \implies (x,y)=(4,2) \end{aligned}\] For \(y=3\): \[\begin{aligned} f &= x^2+2(3)^2-6x-8(3) = x^2-6x-6\\ f_x &= 2x-6 = 0 \qquad \implies (x,y)=(3,3) \end{aligned}\] We make a table of values for each critical point we found, along with each vertex.

    Region	\(x\)	\(y\)	\(f\)	Classification
    Interior	\(3\)	\(2\)	\(-17\)	Minimum
    Edge	\(0\)	\(2\)	\(-8\)
    Edge	\(3\)	\(0\)	\(-9\)
    Edge	\(4\)	\(2\)	\(-16\)
    Edge	\(3\)	\(3\)	\(-15\)
    Vertex	\(0\)	\(0\)	\(0\)	Maximum
    Vertex	\(4\)	\(0\)	\(-8\)
    Vertex	\(0\)	\(3\)	\(-6\)
    Vertex	\(4\)	\(3\)	\(-14\)

    So from the table we can conclude that the minimum of the function is \(f=-17\) at the interior point \((3,2)\), and the maximum is \(f=0\) at the vertex \((0,0)\).

    wll 

37. Find the locations and values of the global maximum and minimum of the function \(f(x,y)=\sin(x)\cos(y)\) inside or on the square \(\dfrac{\pi}{4} \le x \le \dfrac{3\pi}{4}\) and \(-\,\dfrac{\pi}{4} \le y \le \dfrac{\pi}{4}\).

    Find the critical points in the interior, the edges, and the vertices. Then compare the values at those points to determine the minimum and maximum of the function. When solving for critical points, be sure \(x\) and \(y\) are within the region.

    The minimum is \(f=0.5\) at all four verticies, and the maximum is \(f=1\) at the interior point \(\left(\dfrac{\pi}{2},0\right)\).

    To find the critical points inside the square, we set the partial derivatives of \(f=\sin(x)\cos(y)\) equal to \(0\) and solve. Notice that \(\cos(y) \neq 0\) on \(-\,\dfrac{\pi}{4} \le y \le \dfrac{\pi}{4}\), and \(\sin(x) \neq 0\) on \(\dfrac{\pi}{4} \le x \le \dfrac{3\pi}{4}\). \[\begin{aligned} f_x = \cos(x)\cos(y) = 0 \qquad \implies x = \dfrac{\pi}{2}\\ f_y = -\sin(x)\sin(y) = 0 \qquad \implies y = 0 \end{aligned}\] The critical point \(\left(\dfrac{\pi}{2},0\right)\) lies within the square.

    Next, we find all the critical points along the edges of the square, represented by \(x=\dfrac{\pi}{4}\), \(x=\dfrac{3\pi}{4}\), \(y=-\,\dfrac{\pi}{4}\), and \(y=\dfrac{\pi}{4}\). We evaluate the function on each edge and then equate the derivative to zero and solve.
    For \(x=\dfrac{\pi}{4}\): \[\begin{aligned} f &= \dfrac{\sqrt{2}}{2}\cos(y)\\ f_y &= -\,\dfrac{\sqrt{2}}{2}\sin(y) &= 0 \qquad \implies (x,y)=\left(\dfrac{\pi}{4},0\right) \end{aligned}\] For \(x=\dfrac{3\pi}{4}\): \[\begin{aligned} f &= \dfrac{\sqrt{2}}{2}\cos(y)\\ f_y &= -\,\dfrac{\sqrt{2}}{2}\sin(y) &= 0 \qquad \implies (x,y)=\left(\dfrac{3\pi}{4},0\right) \end{aligned}\] For \(y=-\,\dfrac{\pi}{4}\): \[\begin{aligned} f &= \dfrac{\sqrt{2}}{2}\sin(x)\\ f_x &= \dfrac{\sqrt{2}}{2}\cos(x) = 0 \qquad \implies (x,y)=\left(\dfrac{\pi}{2},-\,\dfrac{\pi}{4}\right) \end{aligned}\] For \(y=\dfrac{\pi}{4}\): \[\begin{aligned} f &= \dfrac{\sqrt{2}}{2}\sin(x)\\ f_x &= \dfrac{\sqrt{2}}{2}\cos(x) = 0 \qquad \implies (x,y)=\left(\dfrac{\pi}{2},\dfrac{\pi}{4}\right) \end{aligned}\] We make a table of values for each critical point we found, along with each vertex.

    Region	\(x\)	\(y\)	\(f\)	Classification
    Interior	\(\dfrac{\pi}{2}\)	\(0\)	\(1\)	Maximum
    Edge	\(\dfrac{\pi}{4}\)	\(0\)	\(\dfrac{\sqrt{2}}{2} \approx 0.707\)
    Edge	\(\dfrac{3\pi}{4}\)	\(0\)	\(\dfrac{\sqrt{2}}{2} \approx 0.707\)
    Edge	\(\dfrac{\pi}{2}\)	\(-\,\dfrac{\pi}{4}\)	\(\dfrac{\sqrt{2}}{2} \approx 0.707\)
    Edge	\(\dfrac{\pi}{2}\)	\(\,\dfrac{\pi}{4}\)	\(\dfrac{\sqrt{2}}{2} \approx 0.707\)
    Vertex	\(\dfrac{\pi}{4}\)	\(-\,\dfrac{\pi}{4}\)	\(0.5\)	Minimum
    Vertex	\(\dfrac{\pi}{4}\)	\(\dfrac{\pi}{4}\)	\(0.5\)	Minimum
    Vertex	\(\dfrac{3\pi}{4}\)	\(-\,\dfrac{\pi}{4}\)	\(0.5\)	Minimum
    Vertex	\(\dfrac{3\pi}{4}\)	\(\dfrac{\pi}{4}\)	\(0.5\)	Minimum

    So from the table we can conclude that the minimum of the function is \(f=0.5\) at the verticies, and the maximum is \(f=1\) at \(\left(\dfrac{\pi}{2},0\right)\) in the interior.

    wll 

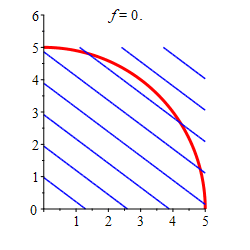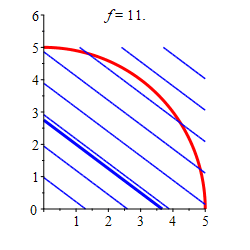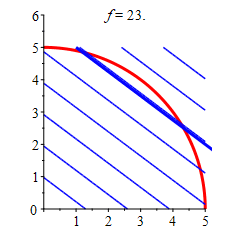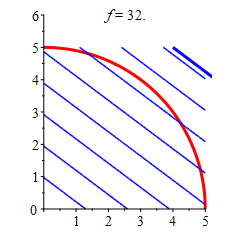
38. Find the locations and values of the global maximum and minimum of the function \(f(x,y)=3x+4y\) inside or on the quarter of the circle \(x^2+y^2=25\) in the \(1^\text{st}\) quadrant.

    Find the critical points in the interior, the edges, and the verticies. Then compare the values at those points to determine the minimum and maximum of the function. Use a combination of Lagrange multipliers and contraint elimination as convenient.

    The minimum of the function in the quarter circle is \(f=0\) at \((0,0)\), and the maximum is \(f=25\) at \((3,4)\) along the arc.

    To find the critical points inside the quarter circle, we set the partial derivatives of \(f=3x+4y\) equal to \(0\) and solve. \[\begin{aligned} f_x = 3 \neq 0 \qquad \\ f_y = 4 \neq 0 \qquad \end{aligned}\] Since there are no solutions, there are no critical points within the quarter circle.
    
    Next, we find all the critical points along the straight edges of the quarter circle, represented by \(x=0\) or \(y=0\). We evaluate the function on each edge and set the derivatve equal to zero.
    For \(x=0\): \[\begin{aligned} f &= 4y\\ f_y &= 4 \neq 0 \end{aligned}\] For \(y=0\): \[\begin{aligned} f &= 3x\\ f_x &= 3 \neq 0 \end{aligned}\] Again this implies that there is no critical point on \(y=0\) or \(x=0\)

    Finally, we look for critical points along the arc of the circle. This will be the point where the level set of \(f=3x+4y\) is tangent to the circle, as shown in the plot. This is best found using Lagrange multipliers. The gradients of the functions are: \[\begin{aligned} \vec\nabla f &=\left(3,4\right) \\ \vec\nabla g &=\left(2x,2y\right) \end{aligned}\] The Lagrange equations, \(\vec\nabla f=\lambda\vec\nabla g\), are

    

    \[\begin{aligned} 3 = \lambda 2x \qquad \text{(1)}\\ 4 = \lambda 2y \qquad \text{(2)} \end{aligned}\] We divide equation (1) by equation (2) to get \(\dfrac{3}{4}=\dfrac{x}{y}\) which implies \(x=\dfrac{3}{4}y\). We plug this into the contraint \(g=x^2+y^2=25\) to get: \[\begin{aligned} \left(\dfrac{3y}{4}\right)^2+y^2&=25 \\ y^2&=16 \\ y&=\pm 4 \end{aligned}\] We use the positive solution, \(y=4\), to solve for \(x\) because our arc is in the first quadrant. \[\begin{aligned} x=\dfrac{3}{4}\cdot 4 =3 \end{aligned}\] So our only critical point is \((3, 4)\). We make a table of values of \(f=3x+4y\) for each critical point and each vertex:

    Region	\(x\)	\(y\)	\(f\)	Classification
    Edge	\(3\)	\(4\)	\(25\)	Maximum
    Vertex	\(0\)	\(0\)	\(0\)	Minimum
    Vertex	\(0\)	\(5\)	\(20\)
    Vertex	\(5\)	\(0\)	\(15\)

    So from the table we can conclude that the minimum of the function in the quarter circle is \(f=0\) at \((0,0)\), and the maximum is \(f=25\) at \((3,4)\) along the arc.

    wll 

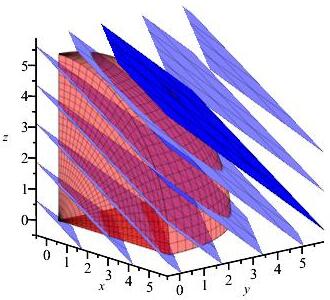
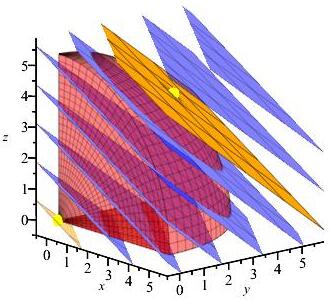
39. Find the locations and values of the global maximum and minimum of the function \(f(x,y,z)=2x+3y+4z\) inside or on the eighth of the sphere \(x^2+y^2+z^2=29\) in the \(1^\text{st}\) octant.

    

    Find the critical points for each volume, surface, and edge. Then compare the values of the functions at those points and the vertices to determine the minimum and maximum. Lagrange multipliers may be useful.

    The minimum of the function in the object is \(f=0\) at \((0,0,0)\), and the maximum is \(f=29\) at \((2,3,4)\).

    We begin by finding critical points within the object (1st octant of a sphere centered at the origin). We set the partial derivatives of \(f=2x+3y+4z\) equal to \(0\) and solve. \[\begin{aligned} f_x = 2 \neq 0 \\ f_y = 3 \neq 0 \\ f_z = 4 \neq 0 \end{aligned}\] Since the derivatives never equal zero, there are no critical points inside the object.

    Next, we find all the critical points along the flat surfaces of the object, represented by \(x=0\), \(y=0\), and \(z=0\). We evaluate the function on each surface and set the derivatve equal to zero. \[\begin{aligned} f &= 3y+4z \qquad& f &= 2x+4z \qquad& f &= 2x+3y\\ f_y &= 3 \neq 0 \qquad& f_x &= 2 \neq 0 \qquad& f_x &= 2 \neq 0\\ f_z &= 4 \neq 0 \qquad& f_z &= 4 \neq 0 \qquad& f_y &= 3 \neq 0 \end{aligned}\] This implies that there is no critical point on any of the flat surfaces.

    Next, we can use Lagrange multipliers with the contraint surface \(g=x^2+y^2+z^2=29\) to find critical points along the spherical surface of the object. The gradients of the functions are: \[\begin{aligned} \vec\nabla f &=\langle 2,3,4 \rangle \\ \vec\nabla g &=\langle 2x,2y, 2z\rangle \end{aligned}\] The Lagrange equations, \(\vec\nabla f=\lambda\vec\nabla g\), are \[\begin{aligned} 2 = \lambda 2x \qquad \text{(1)}\\ 3 = \lambda 2y \qquad \text{(2)}\\ 4 = \lambda 2z \qquad \text{(3)}\\ \end{aligned}\] We divide equations (1) and (2) by equation (3) and solve in terms of \(z\). \[\begin{aligned} \dfrac{2}{4}=\dfrac{x}{z} &\implies x = \dfrac{z}{2} \qquad& \text{(5)}\\ \dfrac{3}{4}=\dfrac{y}{z} &\implies y = \dfrac{3z}{4} \qquad& \text{(6)} \end{aligned}\] We plug these into the contraint \(g=x^2+y^2+z^2=29\) \[\begin{aligned} \left(\dfrac{z}{2}\right)^2+\left(\dfrac{3z}{4}\right)^2+z^2&=29 \\ z^2&=16 \\ z&=\pm 4 \end{aligned}\] We use the positive solution, \(z=4\), to solve for \(x\) and \(y\) because our object is in the first octant. \[\begin{aligned} x&=\dfrac{1}{2}\cdot 4&=2\\ y&=\dfrac{3}{4}\cdot 4&=3 \end{aligned}\] So the critical point on the spherical surface is \((2, 3, 4)\).

    Next, we must find the critical points along the edges of the object. The straight edges are represented by \((x,0,0)\), \((0,y,0)\), and \((0,0,z)\). We evaluate the function at these lines and set the derivatives equal to zero. \[\begin{aligned} f &= 2x \qquad& f &= 3y \qquad& f &= 4z\\ f_x &= 2 \neq 0 \qquad& f_y &= 3 \neq 0 \qquad& f_z &= 4 \neq 0 \end{aligned}\] Since the derivatives never equal zero, there are no critical points along the straight edges.

    Next, we use Lagrange multipliers to find the critical points along the curved edges.
    For \(x=0\), \(f=3y+4z\) on \(g=y^2+z^2=29\). The Lagrange equations say: \[ 3=\lambda2y \qquad 4=\lambda2z \implies y=\dfrac{3z}{4} \] So the constraint says: \[\begin{aligned} \left(\dfrac{3z}{4}\right)^2+z^2&=29 \implies z = \dfrac{4\sqrt{29}}{5} \\ (x, y, z) &= \left(0, \dfrac{3\sqrt{29}}{5},\dfrac{4\sqrt{29}}{5}\right) \end{aligned}\] For \(y=0\), \(f=2x+4z\) on \(g=x^2+z^2=29\). The Lagrange equations say: \[ 2=\lambda2x \qquad 4=\lambda2z \implies x=\dfrac{z}{2} \] So the constraint says: \[\begin{aligned} \left(\dfrac{z}{2}\right)^2+z^2&=29 \implies z = 2 \sqrt{\dfrac{29}{5}} \\ (x, y, z) &= \left(\sqrt{\dfrac{29}{5}}, 0,2 \sqrt{\dfrac{29}{5}}\right) \end{aligned}\] For \(z=0\), \(f=2x+3y\) on \(g=x^2+y^2=29\). The Lagrange equations say: \[ 2=\lambda2x \qquad 3=\lambda2y \implies y=\dfrac{3x}{2} \] So the constraint says: \[\begin{aligned} x^2+\left(\dfrac{3x}{2}\right)^2&=29 \implies x = 2 \sqrt{\dfrac{29}{13}} \\ (x, y, z) &= \left(2 \sqrt{\dfrac{29}{13}}, 3 \sqrt{\dfrac{29}{13}},0\right) \end{aligned}\] We make a table of values of \(f=2x+3y+4z\) for each critical point we found, along with each vertex.

    Region	\(x\)	\(y\)	\(z\)	\(f\)	Classification
    Surface	\(2\)	\(3\)	\(4\)	\(29\)	Maximum
    Edge	\(0\)	\(\dfrac{3\sqrt{29}}{5}\)	\(\dfrac{4\sqrt{29}}{5}\)	\(5\sqrt{29}\approx 26.9\)
    Edge	\(\sqrt{\dfrac{29}{5}}\)	\(0\)	\(2\sqrt{\dfrac{29}{5}}\)	\(2\sqrt{145}\approx 24.1\)
    Edge	\(2 \sqrt{\dfrac{29}{13}}\)	\(3 \sqrt{\dfrac{29}{13}}\)	\(0\)	\(\sqrt{377}\approx 19.4\)
    Vertex	\(\sqrt{29}\)	\(0\)	\(0\)	\(2\sqrt{29}\approx 10.8\)
    Vertex	\(0\)	\(\sqrt{29}\)	\(0\)	\(3\sqrt{29}\approx 16.2\)
    Vertex	\(0\)	\(0\)	\(\sqrt{29}\)	\(4\sqrt{29}\approx 21.5\)
    Vertex	\(0\)	\(0\)	\(0\)	\(0\)	Minimum

    So from the table, we can conclude that the minimum of the function is \(f=0\) at the vertex \((0,0,0)\), and the maximum is \(f=29\) at the point \((2,3,4)\) on the spherical surface. In the plot, the level sets of \(f\) are the planes in blue or orange. The upper orange level set is for \(f=29\) which is tangent to the sphere at \((2,3,4)\). The lower orange level set is for \(f=0\) which passes through the point \((0,0,0)\). All the points in the interior have values of \(f\) between \(0\) and \(29\).

    

    wll,tj 

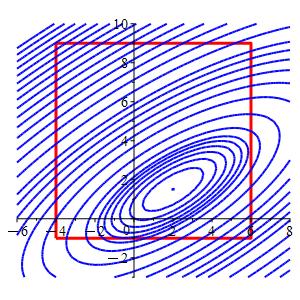
40. Consider the function \(f(x,y)=2x^2-4xy-2x+4y^2-4y\) and the square \(-4 \le x \le 6\) and \(-1 \le y \le 9\).

    In the plot, the square is red and the level sets of \(f\) are blue.

    

    1. Find the locations and values of the global maximum and minimum of the function \(f\) on the (edges of the) square.

       Find the critical points on each edges. Then make a table of the values of \(f\) at those points and the vertices to determine the minimum and maximum locations. When solving for critical points, be sure \(x\) and \(y\) are within the region.

       Global Maximum: \[ f=472 \quad \text{at the vertex} \quad (x,y)=(-4,9) \] Global Minimum: \[ f=7.5 \quad \text{at the edge point} \quad (x,y)=\left(-\,\dfrac{1}{2},-1\right) \]

       We find the critical points along all the edges of the square, represented by \(x=-4\), \(x=6\), \(y=-1\), and \(y=9\). We evaluate the function on each edge and then equate the derivative to zero and solve.
       For \(x=-4\): \[\begin{aligned} f &= 2(-4)^2-4(-4)y-2(-4)+4y^2-4y = 4y^2 +12y +40\\ f_y &= 8y + 12= 0 \qquad \implies (x,y)=\left(-4,\dfrac{-3}{2}\right) \end{aligned}\] This is not on the edge of the square because \(y=\dfrac{-3}{2}\) does not satisfy \(-1 \le y \le 9\).
       For \(x=6\): \[\begin{aligned} f &= 2(6)^2-4(6)y-2(6)+4y^2-4y = 4y^2 -28y +60\\ f_y &= 8y - 28 = 0 \qquad \implies (x,y)=\left(6,\dfrac{7}{2}\right) \end{aligned}\] For \(y=-1\): \[\begin{aligned} f &= 2x^2-4x(-1)-2x+4(-1)^2-4(-1) = 2x^2 +2x + 8\\ f_x &= 4x+ 2= 0 \qquad \implies (x,y)=\left(\dfrac{-1}{2},-1\right) \end{aligned}\] For \(y=9\): \[\begin{aligned} f &= 2x^2-4x(9)-2x+4(9)^2-4(9) = 2x^2 -38x +288\\ f_x &= 4x -38= 0 \qquad \implies (x,y)=\left(\dfrac{19}{2},9\right) \end{aligned}\] This is not on the edge of the square because \(x=\dfrac{-19}{2}\) does not satisfy \(-4 \le x \le 6\).

       We make a table of values of \(f=2x^2-4xy-2x+4y^2-4y\) for each critical point we found, along with each vertex:

       Region	\(x\)	\(y\)	\(f\)	Classification
       Edge	\(6\)	\(\dfrac{7}{2}\)	\(11\)
       Edge	\(\dfrac{-1}{2}\)	\(-1\)	\(7.5\)	Minimum
       Vertex	\(-4\)	\(-1\)	\(32\)
       Vertex	\(-4\)	\(9\)	\(472\)	Maximum
       Vertex	\(6\)	\(-1\)	\(92\)
       Vertex	\(6\)	\(9\)	\(132\)

       So from the table we conclude that the minimum of the function in the square is \(f=7.5\) at the edge point \(\left(-\,\dfrac{1}{2},-1\right)\), and the maximum is \(f=472\) at the vertex \((-4,9)\).

       In the animation, the square is red,
       and the level sets of \(f\) are blue.
       The level sets for the minimum and maximum on the square flash in orange.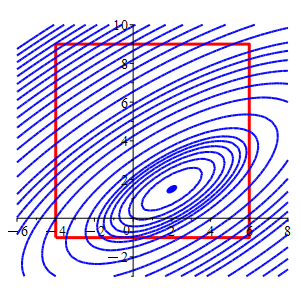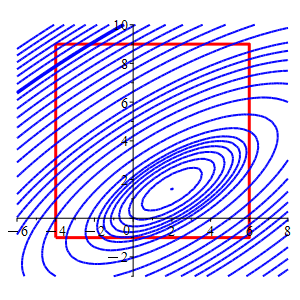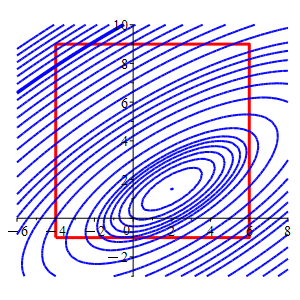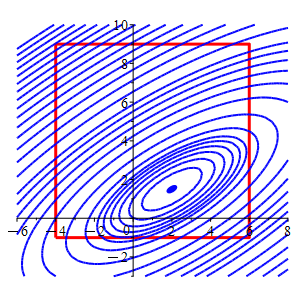

       

       wll,tj 

    2. Find the locations and values of the global maximum and minimum of the function \(f\) inside and on the square.

       Find the critical points in the interior and the edges. Then make a table of the values of \(f\) at those points and the vertices to determine the minimum and maximum locations. When solving for critical points, be sure \(x\) and \(y\) are within the region.

       Global Maximum: \[ f=472 \quad \text{at the interior point} \quad (x,y)=(-4,9) \] Global Minimum: \[ f=-5 \quad \text{at the vertex} \quad (x,y)=\left(2, \dfrac{3}{2}\right) \]

       To find the critical points inside the square, we set the partial derivatives of \(f=2x^2-4xy-2x+4y^2-4y\) equal to \(0\) and solve. \[\begin{aligned} f_x &= 4x-4y-2 &= 0 \\ f_y &= -4x+8y-4 &= 0 \end{aligned}\] We add the two equations to eliminate \(x\) terms, producing the equation \(4y-6=0\). This implies that our critical point is \((x,y)=\left(2, \dfrac{3}{2}\right)\) which we observe is inside the square.

       We add this to the table of values we found in part (a):

       Region	\(x\)	\(y\)	\(f\)	Classification
       Interior	\(2\)	\(\dfrac{3}{2}\)	\(-5\)	Minimum
       Edge	\(6\)	\(\dfrac{7}{2}\)	\(11\)
       Edge	\(\dfrac{-1}{2}\)	\(-1\)	\(7.5\)
       Vertex	\(-4\)	\(-1\)	\(32\)
       Vertex	\(-4\)	\(9\)	\(472\)	Maximum
       Vertex	\(6\)	\(-1\)	\(92\)
       Vertex	\(6\)	\(9\)	\(132\)

       So from the table we can conclude that the minimum of the function in or on the square is \(f=-5\) at the interior point \(\left(2, \dfrac{3}{2}\right)\), and the maximum is \(f=472\) at the vertex \((-4,9)\).

       In the animation, the square is red,
       and the level sets of \(f\) are blue.
       The level sets for the minimum and maximum in or on the square flash in orange.
       The level set which just touches the square also flashes orange, but is no longer the minimum.

       

       wll,tj 

d. Multiple Constraint Problems (Optional)

1

41. The plane \(x+2y+3z =1\) intersects the cylinder \(x^2+y^2=1\) in an ellipse. Find the points on this ellipse closest and farthest from the origin.

    1. Solve using Lagrange multipliers.

    2. Solve using a paramaterization.

    

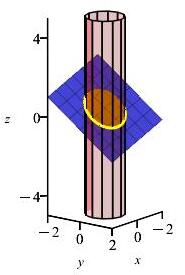
    Simplify your calculations by optimizing the squared distance. Find the gradients of the distance squared and the two contraints. Then, solve the Lagrange equations, \(\vec\nabla f=\lambda\vec\nabla g + \mu\vec\nabla h\), along with the constraints to find critical points. Finally, make a table of values to determine the distances of the critical points found.

    The points closest to the origin is \((1,0,0)\) and \(\left(-\dfrac{3}{5},\dfrac{4}{5},0\right)\). The point farthest from the origin is \(\left(- \dfrac{1}{\sqrt{5}}, - \dfrac{2}{\sqrt{5}}, \dfrac{1 + \sqrt{5}}{3}\right)\).

    We minimize the square of the distance function from the origin using \(f=D^2 = x^2+y^2+z^2\) on the intersection of the plane \(g=x+2y+3z =1\) and the cylinder \(h=x^2+y^2=1\) The gradients of the functions are \[\begin{aligned} \vec\nabla f&=\langle 2x, 2y, 2z \rangle \\ \vec\nabla g&=\langle 1,2,3 \rangle \\ \vec\nabla h&=\langle 2x,2y,0 \rangle \end{aligned}\] The Lagrange equations, \(\vec\nabla f=\lambda\vec\nabla g + \mu\vec\nabla h\), are \[\begin{aligned} 2x&=\lambda + \mu 2x \qquad& \text{(1)} \\ 2y&=\lambda 2 + \mu 2y \qquad& \text{(2)} \\ 2z&=\lambda 3 \qquad& \text{(3)} \end{aligned}\] Equation (3) implies \(\lambda=\dfrac{2}{3}z\) and we eliminate \(\lambda\) by plugging it into equations (1) and (2). \[\begin{aligned} 2x&=\dfrac{2}{3}z + \mu 2x \qquad& \text{(4)} \\ 2y&=\dfrac{4}{3}z + \mu 2y \qquad& \text{(5)} \end{aligned}\] To eliminate \(\mu\), we multiply equation (4) by \(y\) and equation (5) by \(x\) and subtract. This yields: \[ 0=\left(\dfrac{2}{3}y-\dfrac{4}{3}x\right)z \] There are two scenarios, where \(z=0\), or \(\left(\dfrac{2}{3}y-\dfrac{4}{3}x\right)=0\). We use both constraints to find critical points.
    Case 1: \(z=0\) \[\begin{aligned} \begin{array}{r} x+2y=1 \\ x^2+y^2=1 \end{array} \implies \begin{array}{l} x=1-2y \\ (1-2y)^2+y^2=1 \end{array} \implies \begin{array}{l} x=1-2y \\ -4y+5y^2=0 \end{array} \end{aligned}\] The last equation says \(y = 0\) or \(y=\dfrac{4}{5}\). Then \(x=1\) or \(x=-\dfrac{3}{5}\) respectively. So the two critical points are: \[ (x,y,z) = (1,0,0) \qquad \text{and} \qquad \left(-\dfrac{3}{5},\dfrac{4}{5},0\right) \] Case 2: \(\dfrac{2}{3}y-\dfrac{4}{3}x=0\) or equivalently \(y = 2x\) \[\begin{aligned} \begin{array}{r} 5x+3z=1& \\ 5x^2=1& \end{array} \implies \begin{array}{l} x = \pm \dfrac{1}{\sqrt{5}} \quad \text{and} \quad y = \pm \dfrac{2}{\sqrt{5}} \\ 3z=1-5\left(\pm \dfrac{1}{\sqrt{5}}\right)\quad \text{or} \quad z=\dfrac{1 \mp \sqrt{5}}{3} \end{array} \end{aligned}\] So the two critical points are: \[ (x,y,z) = (\dfrac{1}{\sqrt{5}}, \dfrac{2}{\sqrt{5}}, \dfrac{1-\sqrt{5}}{3}) \qquad \text{and} \qquad \left(-\,\dfrac{1}{\sqrt{5}},-\,\dfrac{2}{\sqrt{5}}, \dfrac{1+\sqrt{5}}{3}\right) \] We make a table of values to determine the distance of the critical points.

    \(x\)	\(y\)	\(z\quad\)	\(D^2\)	Classification
    \(1\)	\(0\)	\(0\quad\)	\(1\)	Minimum
    \(-\dfrac{3}{5}\)	\(\dfrac{4}{5}\)	\(0\quad\)	\(1\)	Minimum
    \(\dfrac{1}{\sqrt{5}}\)	\(\dfrac{2}{\sqrt{5}}\)	\(\dfrac{1 - \sqrt{5}}{3}\quad\)	\(\dfrac{15 - 2\sqrt{5}}{9}\approx 1.17\)
    \(-\dfrac{1}{\sqrt{5}}\)	\(-\dfrac{2}{\sqrt{5}}\)	\(\dfrac{1 + \sqrt{5}}{3}\quad\)	\(\dfrac{15 + 2\sqrt{5}}{9}\approx 2.16\)	Maximum

    So from the table, we conclude that the points closest to the origin is \((1,0,0)\) and \(\left(-\dfrac{3}{5},\dfrac{4}{5},0\right)\). The point farthest from the origin is \(\left(- \dfrac{1}{\sqrt{5}}, - \dfrac{2}{\sqrt{5}}, \dfrac{1 + \sqrt{5}}{3}\right)\).

    wll,tj 

    Simplify your calculations by optimizing the squared distance. Start by paramaterizing the cylinder in the \(x\)-\(y\) plane.

    The points closest to the origin is The point farthest from the origin is

    Using cyclindrical coordinates, we can paramaterize \(f=D^2\) on the ellipse. Since the raidus of the cylinder is \(r=1\): \[\begin{aligned} x = \cos\theta \\ y = \sin\theta \end{aligned}\] We use the plane equation to solve for \(z\) and paramaterize: \[\begin{aligned} z&=\dfrac{1-x-2y}{3} \\ z&=\dfrac{1-\cos\theta-2\sin\theta}{3} \end{aligned}\] Substituting these values into \(f=D^2=x^2+y^2+z^2\): \[\begin{aligned} f &= \cos^2\theta + \sin^2\theta + \left(\dfrac{1-\cos\theta-2\sin\theta}{3}\right)^2 \\ &= 1 + \left(\dfrac{1-\cos\theta-2\sin\theta}{3}\right)^2 \end{aligned}\] To find the critical points We differentiate \(f\) and equate it to zero: \[\begin{aligned} f' = 2\left(\dfrac{1-\cos\theta-2\sin\theta}{3}\right) \cdot \left(\dfrac{\sin\theta-2\cos\theta}{3}\right) &= 0 \\ (1-\cos\theta-2\sin\theta) \cdot (\sin\theta-2\cos\theta) &= 0 \end{aligned}\] Case 1: \(1-\cos\theta-2\sin\theta=0\) \[\begin{aligned} 1-\cos\theta-2\sin\theta &= 0 \\ 1 - \cos\theta &= 2\sin\theta \\ (1 - \cos\theta)^2 &= 4\sin^2\theta \\ 1 - 2\cos\theta + \cos^2\theta &= 4(1-\cos^2\theta) \\ 5\cos^2\theta - 2\cos\theta - 3 &= 0 \\ (5\cos\theta+3)(\cos\theta-1) &= 0 \\ \cos\theta &= 1, \dfrac{-3}{5} \\ \theta &= 0, \arccos{\dfrac{-3}{5}} \end{aligned}\] Case 2: \(\sin\theta-2\cos\theta=0\) \[\begin{aligned} \sin\theta-2\cos\theta &= 0 \\ \sin\theta &= 2\cos\theta \\ \tan\theta &= 2 \\ \theta &= \arctan(2), \arctan(2) + \pi \end{aligned}\] We make a table of values of \(D^2=1+\left(\dfrac{1-\cos\theta-2\sin\theta}{3}\right)^2\) to determine the distance of the critical points.

    \(\theta\)	\(D^2\)	Classification
    \(0\)	\(1\)	Minimum
    \(\arccos{\dfrac{-3}{5}}\)	\(1\)	Minimum
    \(\arctan(2)\)	\(1 + \left(\dfrac{1-\sqrt{5}}{3}\right)^2 \approx 1.17\)
    \(\arctan(2) + \pi\)	\(1 + \left(\dfrac{1+\sqrt{5}}{3}\right)^2 \approx 2.16\)	Maximum

    So from the table, we conclude that the points closest to the origin is \((1,0,0)\) and \(\left(-\dfrac{3}{5},\dfrac{4}{5},0\right)\). The point farthest from the origin is \(\left(- \dfrac{1}{\sqrt{5}}, - \dfrac{2}{\sqrt{5}}, \dfrac{1 + \sqrt{5}}{3}\right)\).

    wll,tj 

42. Maximize the function \(f=x^2-y^2+2z\) on the line of intersection of the planes \(y+z=0\) and \(z=2x\).

    Determine the geometry of the constraints and attempt to parameterize the intersection. Maximize the function with respect to the parameterized variable.

    The maximum value of \(f\) at the intersection of the planes \(y+z=0\) and \(z=2x\) is \(\dfrac{4}{3}\).

    To maximize the function \(f=x^2-y^2+2z\), we parameterize the function along the line of intersection of the planes \(y+z=0\) and \(z=2x\), as follows: \[\begin{aligned} x&=t \\ z &= 2x = 2t \\ y &=-z=-2t \end{aligned}\] We plug the parameterized variables into \(f\): \[\begin{aligned} f&=t^2-(-2t)^2+2(2t) \\ &= -3t^2+4t \end{aligned}\] To find the critical points along this intersection, we take the derivatve of \(f\) with respect to \(t\) and equate it to zero: \[ f'=-6t + 4=0 \implies t = \dfrac{2}{3} \] To determine if this is a minimum or maximum, we use the Second Derivative Test. \[ f''=-6 \lt 0 \] Since \(f''\) is always less than zero, the critical point at \(t=\dfrac{2}{3}\) is a maximum. We use \(t\) to get cartesian coordinates and the maximum value of \(f\). \[\begin{aligned} (x,y,z) &= \left(\dfrac{2}{3}, \dfrac{-4}{3},\dfrac{4}{3}\right) \\ f &= -3\left(\dfrac{2}{3}\right)^2+4\left(\dfrac{2}{3}\right) = \dfrac{4}{3} \end{aligned}\] So the maximum value of \(f\) at the intersection of the planes \(y+z=0\) and \(z=2x\) is \(\dfrac{4}{3}\).

    wll 

43. A box manufacturer wants to make a rectangular solid cardboard box to contain \(4000\,\text{cm}^3\). The box is folded from a single rectangular piece of cardboard so that the flaps from \(2\) sides just meet at the centerline of the top and bottom. The flaps from the other \(2\) sides do not need to reach the centerline of the top and bottom. What are the dimensions of the original rectangle of cardboard used to make the box which uses the least amount of cardboard?

    

    Let \(L\) and \(W\) be the length and width of the original piece of cardboard. Let \(x\), \(y\) and \(z\) be the length, width and height of the final box. Write out the constraint for the volume. Write out the constraints relating the original cardboard dimensions to the final box dimensions. What function are you minimizing? How many variables are there? How many constraints?

    The dimensions of the original carboard piece that minimize the amount of cardboard used are: \(L=60\,\text{cm}\) and \(W=30\,\text{cm}\).

    Let \(x\), \(y\) and \(z\) be the length, width and height of the final box, resp. Let \(L\)and \(W\) be the length and width of the original piece of cardboard, resp. The length of the orignal cardboard is the perimeter of the \(xy\) top, so it can be written as \(L=2x+2y\). Similarly, the width of the orignal cardboard is height of the box plus the two flaps which meet exactly in the middle, so it can be written as \(W=\dfrac{y}{2} + z + \dfrac{y}{2} = y + z\). Therefore, the amount of cardboard used is: \[\begin{aligned} A(z, y, x)&=LW= (2x+2y)(y + z) \\ &=2xy+2xz+2y^2+2yz \end{aligned}\] And the total enclosed volume is: \[ V(z,y,x) = xyz = 4000 \] The gradients of the functions are \[\begin{aligned} \vec\nabla A&=\langle 2y+2z,2x+4y+2z,2x+2y \rangle \\ \vec\nabla V&=\langle yz,xz,xy \rangle \end{aligned}\] The Lagrange equations, \(\vec\nabla A=\lambda\vec\nabla V\), are \[\begin{aligned} 2y+2z&= \lambda yz \qquad \text{(1)} \\ 2x+4y+2z&=\lambda xz \qquad \text{(2)} \\ 2x+2y&= \lambda xy \qquad \text{(3)} \end{aligned}\] We multiply equation (1) by \(x\), equation (2) by \(y\), and equation (3) by \(z\). We then equate and solve: \[\begin{aligned} \lambda zyx&= 2xy+2xz=2xy+4y^2+2yz=2xz+2yz \\ &\implies \quad xz = 2y^2+yz \qquad x = z \end{aligned}\] Substituting \(x=z\) into the volume constraint gives: \[\begin{aligned} V &=z^2y=4000\\ y &= \dfrac{4000}{z^2} \\ \end{aligned}\] We substitute this into \(xz = 2y^2+yz\) and solve for \(z\): \[\begin{aligned} z(z) = 2\left(\dfrac{4000}{z^2}\right)^2+\left(\dfrac{4000}{z^2}\right)&(z) \\ z^6-4000z^3&-2(4000)^2 = 0 \end{aligned}\] This is a quadratic equation for \(z^3\). We use the quadratic formula: \[\begin{aligned} z^3 &= \dfrac{4000 \pm \sqrt{4000^2+4\cdot2(4000)^2}}{2} \\ &= 8000\,\text{or} -4000 \\ \end{aligned}\] We take the positive solution \(z^3=8000\). So \(z=20\,\text{cm}\), \(y=10\,\text{cm}\) and \(x=20\,\text{cm}\). So the dimensions of the original carboard piece that minimixes the amount of cardboard used are: \[\begin{aligned} L &= 2x + 2y = 60\,\text{cm} \\ W &= y + z = 30\,\text{cm} \end{aligned}\]

    wll 

Challenge Exercises

It is recommended that you set up the equations using one of the three methods, but then solve them numerically using a Computer Algebra System like Maple or Mathematics or Sage or MatLab.

44. A paper cup has the shape of a frustum of a cone with a bottom. Let the smaller bottom radius be \(r\), the larger top radius be \(R\) and the height be \(h\). If the cup needs to hold \(100\pi\,\text{cm}^3\) of water, what are the dimensions \(r\), \(R\) and \(h\) which use the least paper?

    

    The area of the slanted sides of the cup (frustum) is: \[ A_\text{frustum}=\pi(r+R)\sqrt{(R-r)^2+h^2} \] The area of the bottom is \(A_\text{bottom}=\pi r^2\). So the total area is: \[ A_\text{cup}=\pi(r+R)\sqrt{(R-r)^2+h^2}+\pi r^2 \] The volume of the cup (frustum) is \[ V=\dfrac{1}{3}\pi(r^2+rR+R^2)h \] Add an extra constraint which says the slant height is \[ s^2=(R-r)^2+h^2 \] so then the total area is: \[ A=\pi(r+R)s+\pi r^2 \] This will eliminate a lot of square roots from the problem.

    \[ (r, R, h, s)=(3.10, 5.66, 5.05, 5.66) \]

    From the hint, the surface area of the cup is \[ A=\pi(r+R)s + \pi r^2 \] where the slant height \(s\) satisfies \(s^2=(R-r)^2+h^2\). So we want to minimize the area \(A\) subject to the constraint that the volume is constant: \[ V=\dfrac{1}{3}\pi(r^2+rR+R^2)h=100\pi \] and the constraint on the slant height: \[ G=(R-r)^2+h^2-s^2=0 \] We take the order of the variables in the functions as \((r,R,h,s)\). So the gradients are: \[\begin{aligned} \vec\nabla A&=\langle \pi s + 2\pi r, \pi s, 0, \pi r+ \pi R \rangle \\ \vec\nabla V&=\left\langle \dfrac{\pi h}{3} (2r + R), \dfrac{\pi h}{3} (2R+r), \dfrac{\pi}{3}(r^2+rR+R^2), 0 \right\rangle \\ \vec\nabla G&=\left\langle 2r-2R, 2R-2r, 2h, -2s \right\rangle \end{aligned}\] The Lagrange equations, \(\vec\nabla A=\lambda\vec\nabla V + \mu\vec\nabla G\), are \[\begin{aligned} \pi s + 2\pi r &= \lambda \dfrac{\pi h}{3} (2r+R) + \mu (2r-2R) \qquad &\text{(1)} \\ \pi s &= \lambda \dfrac{\pi h}{3} (2R+r) + \mu (2R-2r) \qquad &\text{(2)} \\ 0 &= \lambda \dfrac{\pi}{3}(r^2+rR+R^2) + \mu 2h \qquad &\text{(3)} \\ \pi r+ \pi R &= -2\mu s \qquad &\text{(4)} \end{aligned}\] From here, we use a CAS system to solve the system of equations. The following python code is used to find a numerical solution:

            
    
          from scipy.optimize import fsolve
          import math as m
    
          def equations(p):
            r, R, h, s, l, u = p
            eq1 = (l * m.pi * h)*(2*r+R)/3 + u*(2*r-2*R) - m.pi *s - 2 * m.pi * r
            eq2 = (l * m.pi * h)*(2*R+r)/3 + u*(2*R-2*r) - m.pi *s
            eq3 = (l * m.pi)*(r**2+r*R+R**2)/3 + 2*u*h
            eq4 = m.pi * r + m.pi * R + 2 * u * s
            eq5 = m.pi * h *(r**2+r*R+R**2)/3 - 100 * m.pi
            eq6 = (R-r)**2 + h**2 -s**2
            return [eq1, eq2, eq3, eq4, eq5, eq6]
    
          print(fsolve(equations, (1, 2, 1, 1, 1, 1)))
    
    
          
        

    We use the initial guess \((1, 2, 1, 1, 1, 1)\) because it is a reasonable set of values for our optimal frustum. It is important to note that your numerical solution may differ depending on your initial conditions. The output of the code produces the values:

          
    
        (3.10, 5.66, 5.05, 5.66, 0.39, -2.43)
    
          
        

    From this output we conclude \[ (r, R, h, s)=(3.10, 5.66, 5.05, 5.66) \] as well as \(\lambda=5.05\) and \(\mu=5.66\). These are plausible dimensions for the frustum, and thus one optimal solution.

    wll,tj 

45. A trash dumpster has the shape shown in the plot. It is a rectangular solid with a triangular prism cut off the top front where there is a diagonal lid. Let \(W\) be the width across the front. Let \(L\) be the length of the base from back to front. Let \(H\) be the height of the back. Let \(\ell\) be the length of the top from the back to the lid. Let \(h\) be the height of the front from the bottom to the lid. The heavy steel base costs $\(40\) per square foot. The sides, top and lid are lighter steel which cost $\(20\) per square foot. Every edge needs to be welded which costs $\(1\) per foot. The hinge for the lid costs $\(10\) per foot including its welding cost. The volume needs to be \(150\,\text{ft}^3\). The lid needs to be \(15\,\text{ft}^2\). What are the dimensions which minimize the total cost? (Solving the resulting equations may require a computer algebra system.)

    

    To eliminate a bunch of square roots, it is helpful to introduce an extra variable which is the slant length of the lid: \[ s=\sqrt{(L-l)^2+(H-h)^2} \] along with the extra constraint: \[ s^2-(L-l)^2-(H-h)^2=0 \] Find the set of Lagrange equations then use a CAS system to find a numerical solution.

    \[ (W, L, H, l, h, s)=(4.65, 4.84, 7.20, 2.56, 4.92, 3.22) \]

    We construct a function for the total cost of construction. First, at $\(40\) per square foot, the base costs: \[ C_{base} = 40WL \] At $\(20\) per square foot, the top, front, back, \(2\) sides, and lid cost: \[\begin{aligned} C_{body}&= 20lW + 20hW + 20HW + 40LH \\ &\quad- 20(L-l)(H-h) + 20W\sqrt{(L-l)^2+(H-h)^2} \end{aligned}\] At $\(10\) per foot, the hinge costs: \[ C_{hinge} = 10W \] At $\(1\) per foot, the welding costs: \[ C_{weld} = 3W + 2L + 2H + 2h + 2l \] So the total cost of the dumpster is: \[\begin{aligned} C&=40WL + 20lW + 20hW + 20HW + 40LH - 20(L-l)(H-h) \\ &\quad+ 20W\sqrt{(L-l)^2+(H-h)^2} + 13W + 2L + 2H + 2h + 2l \end{aligned}\] To simplify the formulas by eliminating square roots, we introduce an extra variable \(s=\sqrt{(L-l)^2+(H-h)^2}\) which is the slant length of the lid. Then the cost simplifies to: \[\begin{aligned} C&=40WL + 20lW + 20hW + 20HW + 40LH - 20(L-l)(H-h) \\ &\quad+ 20Ws + 13W + 2L + 2H + 2h + 2l \end{aligned}\] The total volume of the dumpster is the first constraint: \[ V = WLH - \dfrac{W(L-l)(H-h)}{2} = 150 \] The area of the lid is the second constraint: \[ A = Ws = 15 \] And to account for the extra variable \(s\), we introduce an extra third constraint: \[ G=s^2-(L-l)^2-(H-h)^2=0 \] We take the order of the variables in the functions as \((W, L, H, l, h, s)\). So the gradients are: \[\begin{aligned} \vec\nabla C &=\big\langle 40L + 20l + 20h + 20H + 20s + 13, \\ &\qquad40W + 40H - 20(H-h) + 2, \\ &\qquad20W + 40L - 20(L-l) + 2, \\ &\qquad20W + 20(H-h) + 2, \\ &\qquad20W + 20(L-l) + 2, \\ &\qquad20W \rangle \\ \end{aligned}\] \[\begin{aligned} \vec\nabla V &=\left\langle LH - \dfrac{(L-l)(H-h)}{2}, WH - \dfrac{W(H-h)}{2}, \right. \\ &\qquad \left.WL - \dfrac{W(L-l)}{2}, \dfrac{W(H-h)}{2}, \dfrac{W(L-l)}{2}, 0 \right\rangle \\ \end{aligned}\] \[\begin{aligned} \vec\nabla A &=\big\langle s, 0, 0, 0, 0, W \big\rangle \end{aligned}\] \[\begin{aligned} \vec\nabla G &=\big\langle 0, -2(L-l), -2(H-h), 2(L-l), 2(H-h), 2s \big\rangle \end{aligned}\] The Lagrange equations, \(\vec\nabla C=\lambda\vec\nabla V+\mu\vec\nabla A+\kappa\vec\nabla G\), are \[\begin{aligned} 40L + 20l + 20h + 20H + 20s + 13 &=\lambda (LH - \dfrac{(L-l)(H-h)}{2}) + \mu(s) + \kappa (0) \qquad &\text{(1)} \\ 40W + 40H - 20(H-h) + 2 &=\lambda (WH - \dfrac{W(H-h)}{2}) + \mu (0) + \kappa (-2(L-l)) \qquad &\text{(2)} \\ 20W + 40L - 20(L-l) + 2 &=\lambda (WL - \dfrac{W(L-l)}{2}) + \mu (0) + \kappa (-2(H-h)) \qquad &\text{(3)} \\ 20W + 20(H-h) + 2 &=\lambda\dfrac{W(H-h)}{2} + \mu (0) + \kappa (2(L-l)) \qquad &\text{(4)} \\ 20W + 20(L-l) + 2 &=\lambda\dfrac{W(L-l)}{2} + \mu (0) + \kappa (2(H-h)) \qquad &\text{(5)} \\ 20W &=\lambda (0) + \mu (W) + \kappa (2s) \qquad &\text{(6)} \end{aligned}\] From here, we use a CAS system to solve the system of \(9\) equations (\(6\) from Lagrange and \(3\) constraints) in \(9\) unknowns (\(W,L,H,l,h,s,\lambda,\mu,\kappa\)). The following python code is used to find a numerical solution:

            
    
        def equations(p):
            W, L, H, l, h, s, lam, mu, kap = p
            eq1 = 40*L + 20*l + 20*h + 20*H + 20*s + 13 - lam*(L*H-(L-l)*(H-h)/2) - mu*s - kap*0
            eq2 = 40*W + 40*H - 20*(H-h) + 2 - lam*(W*H - W*(H-h)/2) - mu*(0) - kap*(-2*(L-l))
            eq3 = 20*W + 40*L - 20*(L-l) + 2 - lam*(W*L - W*(L-l)/2) - mu*(0) - kap*(-2*(H-h))
            eq4 = 20*W + 20*(H-h) + 2 - lam*(W*(H-h)/2) - mu*(0) - kap*(2*(L-l))
            eq5 = 20*W + 20*(L-l) + 2 - lam*(W*(L-l)/2) - mu*(0) - kap*(2*(H-h))
            eq6 = 20*W - lam*(0) - mu*(W) - kap*(2*s)
            eq7 = W*L*H - W*(L-l)*(H-h)/2 - 150
            eq8 = W*s - 15
            eq9 = s**2 - (L-l)**2 - (H-h)**2
            return [eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9]
    
        print(fsolve(equations, (4, 4, 4, 1, 1, 1, 1, 1, 1)))
    
          
        

    We use the initial guess \((4, 4, 4, 1, 1, 1, 1, 1, 1)\) because it is a plausible set of values for our optimal dumpster. It is important to note that your numerical solution may differ depending on your initial conditions. The output of the code produces the values:

          
    
            [4.65, 4.84, 7.20, 2.56, 4.92, 3.22, 17.04, 4.72, 11.03]
    
          
        

    From this output we conclude \[ (W, L, H, l, h, s)=(4.65, 4.84, 7.20, 2.56, 4.92, 3.22) \] as well as \(\lambda=17.04\), \(\mu=4.72\), and \(\kappa=11.03\). These are plausible dimensions for the dumpster, and thus one optimal solution.

    wll,tj 

PY: Checked to here except 20 plot.